- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2012
- Dynamics and extreme conditions
- Microscopic and mesoscopic structure of functional perovskite ferroelectrics
Microscopic and mesoscopic structure of functional perovskite ferroelectrics
Piezoelectric materials change their physical dimensions under application of an electric voltage and generate voltage under mechanical stress. Today they are widely used as sensors and actuators in various industries. In general, the most efficient piezoelectrics are mixed perovskites with composition close to the so-called morphotropic phase boundary (MPB). Near the MPB the ferroelectric phases of different symmetry have nearly the same energy and are separated by a rather small potential barrier. As a result, the different states can be easily switched by a small electrical or mechanical signal providing high electromechanical coupling. The exact structure and switching mechanisms are, however, challengingly complex and not yet understood. We combine diffuse and inelastic X-ray scattering experiments to reveal the character of structural heterogeneity in the most extensively used MPB piezoelectric – PZT.
Lead zirconate-titanate PbZr1-xTixO3 (PZT) holds about 80% of the piezoelectric market. It is also a model system for studying the MPB phenomenon, which is observed for compositions when x is around 0.48. Many diffraction studies have been devoted to understanding the structure of PZT near the MPB, but despite these efforts, the results and their interpretation remain controversial [1]. This is mainly due to the fact that diffraction studies reveal in almost all cases a structure, which is more complex than the single phase long-range ferroelectric order. The real microscopic structure can be studied effectively by analysing the scattering outside Bragg peaks by diffuse and inelastic scattering methods. We used these methods at beamlines BM01A and ID28, respectively. PZT single crystals of sufficient size and quality were grown at the Simon Frazer University (Canada).
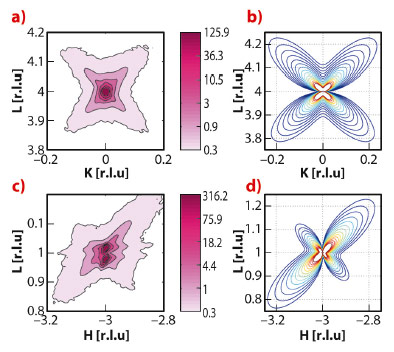
Our diffraction measurements reveal the appearance of strong anisotropic diffuse scattering around Bragg spots (Figure 47 a,c) at temperatures just below the transition between two different ferroelectric phases (about T = 430 K). The observed scattering does not correspond to the polarisation fluctuations near the phase transition because it is absent on the high-temperature side of the ferroelectric-ferroelectric transition and also near the ferroelectric-paraelectric transition (about T = 663 K). Consequently, we have to assume another mechanism, which takes into account some structural inhomogeneity.
 |
|
Fig. 47: Experimental diffuse scattering maps (a,c) and corresponding calculations (b,d) |
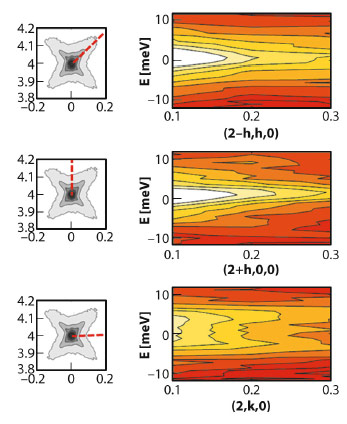
To further understand the origin of diffuse scattering we used inelastic X-ray scattering (IXS). This technique allows static and dynamic components of diffuse scattering to be disentangled due to the meV energy analysis of the scattered photons. Figure 48 schematically shows the IXS intensity maps along the inspected directions in reciprocal space. We observe strong quasielastic scattering (centred at zero energy-transfer) in diagonal and longitudinal directions, while in transverse directions the scattering is almost purely inelastic. Therefore, the observed diffuse scattering (Figure 47a) is a superposition of two contributions: one is due to phonons and the other one is due to static deviations from long-range order. The important feature of this second component is the absence of any intensity along the transverse direction. To reproduce this feature with models by considering the diffuse scattering as a Fourier image of real-space objects or 3D correlators was not possible. In contrast, it is consistent with Huang scattering – scattering due to inhomogeneous deformations of the lattice. More specifically, we note a very good agreement (Figure 47 b,d) with experimental data when the deformations are modelled as being due to tetragonal-symmetry point defects in a matrix that is nearly cubic. From the anisotropy of the diffuse scattering, it can be deduced that these defects produce very small volume strain due to the specific ratio between tensile strain along the main tetragonal direction and compressive strain along the two other directions. The emerging physical picture behind this model assumes that small clusters of the tetragonal phase remain in the matrix of the new average structure below the ferroelectric-ferroelectric phase transition temperature. In this model we associate the diffuse scattering with the scattering by the matrix surrounding the clusters (not with the scattering by the clusters themselves, which are too small for direct observation) because the matrix is deformed on a larger, mesoscopic scale.
 |
|
Fig. 48: Inelastic X-ray scattering maps along the three key directions of the (0 0 2) Brillouin zone. |
Last, but not least, the observed morphotropic PZT diffuse scattering appears at first sight to be very similar in shape to that of relaxor ferroelectrics [2] – a different and special class of disordered perovskites. However there are clear topological differences with respect to the relaxor case – in (0 0 L) Brillouin zones of PZT the transverse diffuse scattering component is suppressed, while for diffuse scattering in relaxors, the minimum of intensity appears along the longitudinal direction. This forms a solid basis for the assumption that the origin of diffuse scattering in these two classes of materials is also different. We believe that the present work on PZT will further stimulate the development of a common understanding of disorder phenomena in functional perovskite ferroelectrics.
Principal publication and authors
R.G. Burkovsky (a,b), Y.A. Bronwald (a), A.V. Filimonov (a), A.I. Rudskoy (a), D. Chernyshov (c), A. Bosak (b), J. Hlinka (d), X. Long (e), Z.-G. Ye (e) and S. Vakhrushev (f,a), Phys. Rev. Lett. 109, 097603 (2012).
(a) St. Petersburg State Polytechnical University (Russia)
(b) ESRF
(c) SNBL at ESRF (France)
(d) Institute of Physics, Academy of Sciences of the Czech Republic, Prague (Czech Republic)
(e) Department of Chemistry and 4D LABS, Simon Frazer University, Burnaby (Canada)
(f) Ioffe Physical-Technical Institute, St. Petersburg (Russia)
References
[1] J. Kreisel, B. Noheda and B. Dkhil, Phase Transitions 82, 633 (2009).
[2] A. Bosak, D. Chernyshov, S. Vakhrushev and M. Krisch, Acta Crystallographica A68, 117 (2012).



