- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2009
- Electronic structure and magnetism
- Field-induced magnetostructural phase transition in Ca2FeReO6 studied via XMCD under 30 T pulsed magnetic field
Field-induced magnetostructural phase transition in Ca2FeReO6 studied via XMCD under 30 T pulsed magnetic field
Ordered double perovskites have attracted substantial attention over the past 10 years due to strong spin polarisation of the electrical carriers and high Curie temperature [1,2]. These properties could lead to the discovery of a material with a reasonable degree of magnetoresistance (MR) at room temperature and so to application of the materials in magnetoelectronics. The most promising series, namely A2FeMoO6, A2FeReO6, A2CrReO6, and A2CrOsO6 (A = alkaline earth metals), are being investigated intensively to find the material with optimal performance. Among the intriguing characteristics of these compounds are the differences in magnetic properties of 4d- and 5d-based analogs despite their almost identical crystal structure. For example, the Re-based double perovskites show strong magnetostructural coupling as well as considerably higher Curie temperature than their Mo-based counterparts. The strong magnetostructural effects are attributed to the interplay between structural degrees of freedom with unquenched Re orbital moment. This interplay is especially pronounced for the compound Ca2FeReO6, which undergoes a metal-insulator (MI) phase transition at TS ~150 K associated with structural deformations of the ReO6 octahedra and redistribution in the Re 5d orbitals occupancy. Neutron diffraction, high-field magnetoresistance, and magnetostriction experiments suggest that at low temperature the two magnetostructural phases, of considerably different electron transport properties, coexist and that their relative population depends on temperature and magnetic field giving rise to large negative magneto-resistance, MR~2000% at T = 100 K [2].
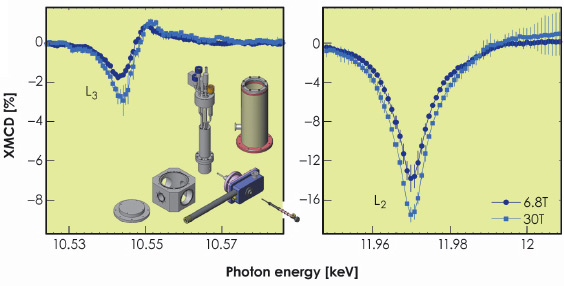
To investigate the role played by the Re orbital moment in the mechanism of the structural phase transition, a high field X-ray magnetic circular dichroism (XMCD) experiment was performed. We studied the field and temperature evolution of the Re orbital (L) and spin (S) components of the magnetic moment derived from L2,3-edge spectra (Figure 93) by means of sum rules. The main challenge was to acquire the spectra at high magnetic field, B > 20 T, in a temperature range wide enough to induce a substantial change in the relative phase fraction. Such experimental conditions have become available only recently, employing the energy-dispersive acquisition technique available at beamline ID24 in combination with a minipulsed field setup [3].
 |
|
Fig. 93: Rhenium L2,3-edge XMCD spectra measured at T = 10 K using the ESRF minipulsed field installation (inset). |
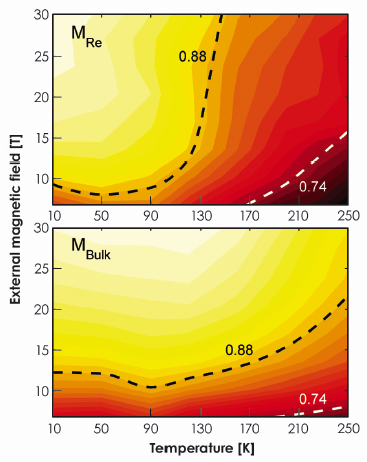
Analysis of the B and T evolution of Re orbital-to-spin magnetic moment ratio gives unequivocal evidence that the two magnetocrystalline phases observed in Ca2FeReO6 are characterised by different spin-orbit coupling. The insulating phase, observed at low temperature and field, is being suppressed by the metallic phase, characterised by larger absolute value of L/S, either upon heating above TS or upon application of a strong magnetic field of several Tesla. The shape comparison of bulk magnetisation with the XMCD derived Re one (Figure 94) reveals a striking difference, which is attributed to electron redistribution between anti-ferromagnetically coupled Re and Fe sites upon temperature and field change. Quantitative analysis revealed that Re magnetisation is significantly higher in the insulating phase with respect to bulk. This gives evidence that the metal-insulator phase transition is accompanied by the evolution in the population of Re t2g orbitals as well as with the charge-transfer between Fe and Re sites. Both effects have a strong influence on the hopping integral of the double-exchange-like interaction between Re and Fe sites and, thus, on the electronic properties of the compound.
 |
|
Fig. 94: Temperature and field evolution of the normalised Re and bulk magnetisations. The latter was adapted from data published in ref. [4]. Increase of magnetisation is denoted by colour change from dark-red to bright-yellow. Smoothed iso-M curves are presented at arbitrary values as guides for the eyes. |
References
[1] K.-I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature (London) 395, 677 (1998).
[2] D. Serrate, J.M. DeTeresa and M.R. Ibarra, J. Phys.: Condens. Matter 19, 023201 (2007).
[3] P. van der Linden, O. Mathon, C. Strohm and M. Sikora, Rev. Sci. Instrum. 79, 075104 (2008).
[4] J.M. Michalik, J.M. DeTeresa, J. Blasco, P.A. Algarabel, M.R. Ibarra, C. Kapusta and U. Zeitler, J. Phys.: Condens. Matter 19, 506206 (2007).
Principal publication and authors
M. Sikora (a), O. Mathon (b), P. van der Linden (b), J.M. Michalik (c), J.M. De Teresa (c), Cz. Kapusta (a), and S. Pascarelli (b), Phys. Rev. B 79, 220402R (2009).
(a) AGH University of Science and Technology, Krakow (Poland)
(b) ESRF
(c) ICMA, Universidad de Zaragoza-CSIC, Zaragoza (Spain)



