- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2008
- Materials science
- Morphological clues to wet granular pile stability
Morphological clues to wet granular pile stability
When dry sand is mixed with water, it acquires a visco-plastic texture, stiff enough for sculpting sand castles. The well-known experience at the beach that the mechanical properties of this material do not depend critically on the liquid content is of great potential importance for understanding wet granular systems in general, such as encountered in land slides, or in the pharmaceutical or food industry. The insignificance of the water content is particularly unexpected if one considers the enormous geometric complexity of the liquid structures which form inside the granular pile, and change dramatically with the liquid content.
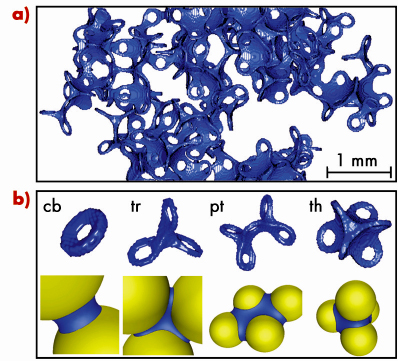
The geometrical structure of the liquid was analysed by means of X-ray microtomography. Owing to the high temporal resolution available at beamline ID15A, inherent ageing problems in the samples could be circumvented and high quality data of highly absorbing static and dynamic samples were obtained. Figure 29a shows an image of a three-dimensional liquid cluster formed in a pile of glass spheres. It turned out that most of the space between the spheres is not filled with liquid, but with air. This can be seen more clearly in Figure 29b, where the smallest liquid morphologies are presented. For liquid contents W < 0.02 only capillary bridges can be found in a wet pile. These morphologies are the building blocks for all larger morphologies, i.e. liquid clusters emerging for W > 0.02 are built from capillary bridges (cb), trimers (tr), or filled tetrahedron gaps “glued together” at their edges. The surface to volume ratio of those extended liquid morphologies was found to be about constant for all observed liquid contents.
 |
|
Fig. 29: a) X-ray microtomography of a liquid cluster in a dense pile of glass beads of 0.8 mm diameter at a liquid content of W ~ 0.11. W is defined with respect to the entire sample volume. b) Smallest liquid morphologies emerging in wet piles of glass beads. Top row: as found by X-ray tomography, bottom row: as calculated numerically. For W < 0.02 only capillary bridges (cb) can be found. For larger liquid contents the capillary bridges might merge to form trimers (tr), pentamers (pt), etc. At low liquid content, filled tetrahedron gaps (th) can also be found. |
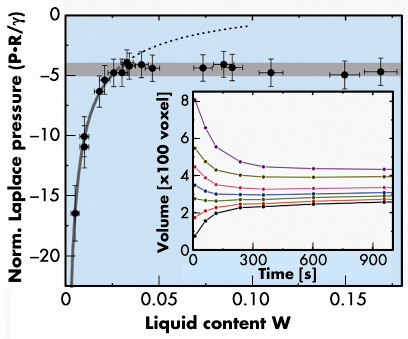
A closer analysis shows that the internal geometry of these intertwined structures of liquid, air, and the grains can be well characterised by a few parameters. In particular, it can be predicted from the packing geometry that the Laplace pressure within equilibrated liquid clusters acquires a universal value for liquid contents, above W ~ 0.02. It should only depend upon the surface tension of the liquid, its wetting angle, and the typical size and shape of the grains. That this is in fact the case is shown in Figure 30, where the Laplace pressure, which could be inferred from the tomographic data, is shown as a function of the liquid content. Over almost the full range of data, it stays at the grey bar, which represents the universal value for the Laplace pressure as derived from the sample parameters. The liquid morphologies equilibrate after a typical time delay of 5 minutes for the beads used in our experiment, as displayed in the inset of Figure 30. Liquid morphologies with a smaller Laplace pressure will grow at the cost of liquid morphologies with larger Laplace pressure. In equilibrium any liquid morphology in the sample will have the same Laplace pressure (see the grey bar in Figure 30).
 |
|
Fig. 30: The Laplace pressure within the liquid clusters, as a function of the liquid content of the sample. The grey bar indicates the universal pressure value calculated from the sample parameters (surface tension and size of spheres), its width corresponds to the uncertainty in the wetting angle. The inset shows the equilibration of individual liquid clusters after preparation. |
This result entails a constant material stiffness over the full range of data, even for small liquid content where the Laplace pressure deviates from the grey bar. In this regime, the wetted area varies as well, but in such a way that the resulting cohesion forces remain constant down to the lowest contents investigated. As a result, the cohesion strength of a wet granular pile is largely independent of liquid content over the full range investigated. We could furthermore present evidence that this general behaviour is also valid for non-spherical granules, like real sand grains.
Principal publications and authors
M. Scheel (a), R. Seemann (a,b), M. Brinkmann (a), M. DiMichiel (c), A. Sheppard (d), B. Breidenbach (e), S. Herminghaus (a), Nature Materials, 7, 189 (2008); J. Phys.: Cond. Mat. 20, 494236 (2008).
(a) Max Planck Institute for Dynamics and Self-Organization, Göttingen (Germany)
(b) Experimental Physics, Saarland University, Saarbrücken (Germany)
(c) ESRF
(d) Department of Applied Mathematics, Australian National University Canberra (Australia)
(e) Theoretical Physics Institute, University Erlangen-Nürnberg, Erlangen (Germany)



