Amongst potential applications of multilayers in third generation synchrotron optics, high-flux monochromators and dedicated focusing devices are the most relevant. In the first case the multilayer acts as a Bragg reflector and one benefits from the about 100 times wider intrinsic bandwidth of a multilayer compared to a perfect crystal. Focusing multilayers require curved substrates and an additional lateral thickness gradient to account for the variation of the Bragg angle. To date, about half of all ESRF beamlines have been equipped with multilayer-based optics, either permanently or for dedicated experiments. Recently, two new devices have been developed and tested.

Double-multilayer Monochromator

A double-reflection multilayer monochromator has been developed at BM5 in order to fulfil two different functions. As a primary monochromator, it provides a higher bandwidth and a higher photon flux than the Si(111) Bragg crystal monochromator. In combination with the crystal monochromator, it rejects harmonics and the beam exit can be kept fixed. An additional aim is to preserve the beam coherence. Optical and geometrical requirements led to the design of two [Ru/B4C]70 multilayers with a d-spacing of 4.0 nm coated on 300 mm long super-polished Si substrates. The fabrication was done at the ESRF Multilayer Laboratory using a sputtering technique. Although the reflecting surfaces are flat, the finite source distance imposed a lateral thickness gradient of about 1% on the d-spacing to obtain a maximum reflectivity over the whole length of the mirror.

 

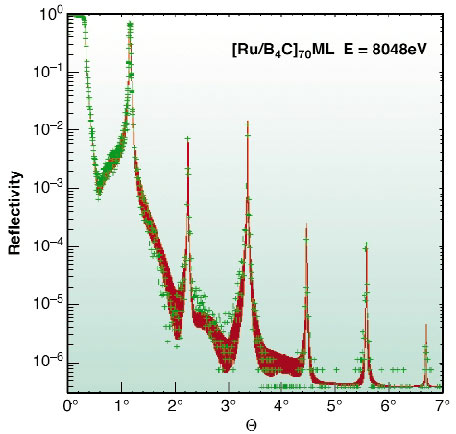
Fig. 167: Measured specular reflectivity versus incidence angle (crosses) and numerical simulation (red curve) of a Ru/B4C multilayer.

 

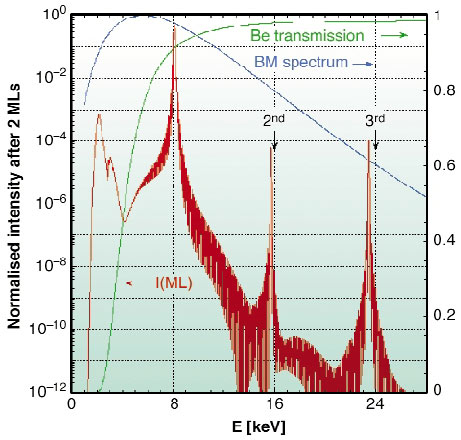
Figure 167 shows the measured specular reflectivity of one multilayer at a photon energy of 8048eV (crosses) superimposed by a simulation (red curve). The latter was then used to calculate the expected performance over a part of the energy range accessible at BM5. Figure 168 illustrates the estimated intensity after two multilayer reflections at a grazing angle of 1.15° (red curve) starting from the bending magnet source spectrum (blue curve), and including the transmission through all Be windows (green curve). The graph shows that, used as a primary monochromator, lower energies and harmonics of the multilayer itself are reduced by a factor of 10-3 to 10-4. In combination with the Si(111) crystal monochromator, the third crystal diffraction harmonic is strongly attenuated, thanks to the pronounced refraction effect that shifts the multilayer Bragg angles (see arrows in Figure 168).

 

Fig. 168: Estimated intensity versus energy after two multilayer reflections (red curve) on a logarithmic scale, taking into account the bending magnet source spectrum (blue curve) and the transmission through all Be windows (green curve), shown on a linear scale.

 

Measurements on BM5 confirm that the flux density is 86 times higher than after the Si(111) monochromator at 17.5 keV, thanks to the high reflectivity (70% for 2 reflections) and to the wider bandpass (2%). At 8 keV, where the beam spectral purity is critical, the multilayers allow the rejection of the Si(111) third harmonic by a factor 210-7. Small substrate or multilayer imperfections would immediately affect the coherence of the X-ray beam after reflection. The Talbot technique allows measurement of the resulting virtual source size increase, by recording diffraction images of a periodic object at different distances [1]. The so-obtained vertical source size of 84 mm corresponds to the values measured without multilayers, showing that the latter do not visibly degrade the beam coherence. The multilayer monochromator has been commissioned as a permanent part of the beamline optics at BM5.

Double-graded Multilayers for Broadband Focusing

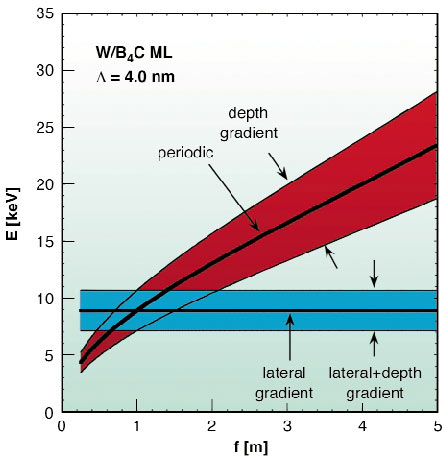
To further increase the effective bandwidth of MLs, non-periodic or depth-graded layered structures can be designed [2]. It would be desirable to merge this approach with the above-mentioned lateral gradient required for curved optics. This would allow the fabrication of a focusing mirror with fixed focal distance and large beam acceptance over a wide energy range. The underlying concept is illustrated in Figure 169 and is similar to that of DuMond diagrams [3]. In the energy dispersion relation E = E() (Bragg equation) the angular dependence has to be interpreted in terms of the distance f from the position on the mirror to the focal spot, that is = (f), thus leading to E = E(f).

 

BM5 monochromator: multilayer mounted on its water-cooled holder.

 

 

Fig. 169: Energy dispersion of different multilayers. Thick solid lines represent periodic multilayers either with or without lateral gradient. A purely depth-graded multilayer covers the red zone. A combination of lateral and depth gradient is indicated by the blue area.

 

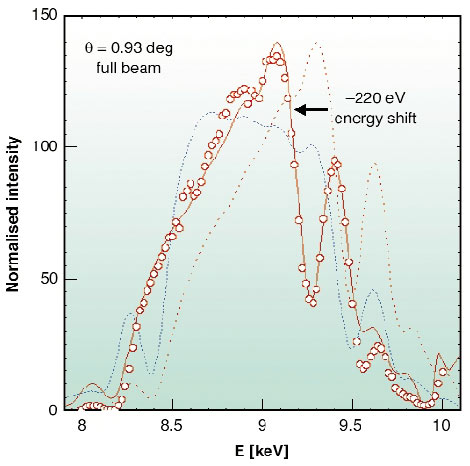
Following this idea, a double-graded focusing multilayer mirror with a length of 270 mm and a focal distance of 285 mm was designed and fabricated at the ESRF Multilayer Laboratory. Based on a W/B4C coating, it should provide a constant reflectivity of 50% in a bandwidth of 9% about a mean energy of 9 keV. Focusing experiments were carried out at APS on the undulator beamline 7ID. The focal line was recorded with a CCD camera while varying the photon energy of the incoming beam. The measured line width remained stable at about 8 µm, mostly limited by the figure error of the bent substrate. The total intensity is plotted in Figure 170 as a function of the photon energy. The experimental data (circles) differ considerably from the ideal prediction (dashed line). However, after inclusion of attenuation and alignment corrections, a good simulation of the data is possible (solid line). We are currently developing a device to be installed at ESRF beamlines.

 

Fig. 170: Normalised total intensity of the focal line measured on the CCD detector (circles) versus photon energy. The dashed blue line indicates the ideal spectrum, the solid red curve is the result after corrections due to absorption and energy shift.

 

References
[1] P. Cloetens, J.-P. Guigay, C. De Martino, J. Baruchel, M. Schlenker, Opt. Lett. 22, 1059 (1997).
[2] Ch. Morawe, E. Ziegler, J.-Ch. Peffen, I.V. Kozhevnikov, Nucl. Instr. and Meth. A 493, 189 (2002).
[3] J.W.M. DuMond, Phys. Rev. 52, 872 (1937).

Principal publications and authors
Th. Bigault (a), E. Ziegler (a), Ch. Morawe (a), R. Hustache (a), J.-Y. Massonat (a), G. Rostaing (a), SPIE Proceedings 5195 (2003); Ch. Morawe (a), J.-Ch. Peffen (a), E.M. Dufresne (b), Y.S. Chu (c), A.T. Macrander (c), SPIE Proceedings 5195 (2003).
(a) ESRF
(b) University of Michigan (USA)
(c) APS (USA)