- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2001
- Surfaces, Interfaces and Nano-science
- Non-dipolar Effects in X-ray Photoemission Investigated with X-ray Standing Waves
Non-dipolar Effects in X-ray Photoemission Investigated with X-ray Standing Waves
The analysis of photoelectron spectroscopy data is commonly based on the dipole approximation, where the radial extent of the electron wavefunction is neglected in the scattering matrix element
<f | exp(ikr) (ep) | i>,
and only the first term in the expansion of the exponential is considered, i.e. exp(ikr) = 1. Here e is the polarisation vector and p the momentum operator. This approximation is valid as long as the wavelength used is large, i.e. the magnitude of k is small compared to r, but becomes questionable at short X-ray wavelengths. X-ray photoemission spectroscopy (XPS) at shorter X-ray wavelengths is now attracting more and more interest because it can provide an opportunity to enhance the electron mean free path, which is only about 0.5 nm for an electron kinetic energy of 50 eV, in contrast to about 5 nm at 10 keV. As a result, the inherent surface sensitivity of photoemission can be overcome. Obtaining the predominantly bulk electronic information in this way is considered as one of the future scientific goals and directions of research at the ESRF and ID32. Thus, the contribution of higher-order multipole terms (exp(ikr) = 1 + ikr +- ...) to the scattering matrix element needs to be understood. Furthermore, the investigations of multipole terms have attracted interest in the past since they allow a deeper understanding of the atomic processes governing photoemission. Unfortunately, measurements of multipole contributions using just one X-ray beam are technically difficult and existing results exhibit quite large margins of error.
The X-ray standing wave (XSW) technique is one of the most precise tools for the determination of surface structures and adsorbate sites. As shown schematically in Figure 60, it exploits the yield, Y, of a spectroscopic signal characteristic for the adsorbate (such as photoelectrons, Auger electrons, or X-ray fluorescence). Usually, XSW data are analysed using the dipole approximation for the spectroscopic signal. However, if multipole contributions are neglected for the analysis of XPS/XSW data, the result may be seriously wrong. Fortunately, as shown in [1], the XSW technique can also be used to accurately determine the multipole contributions.
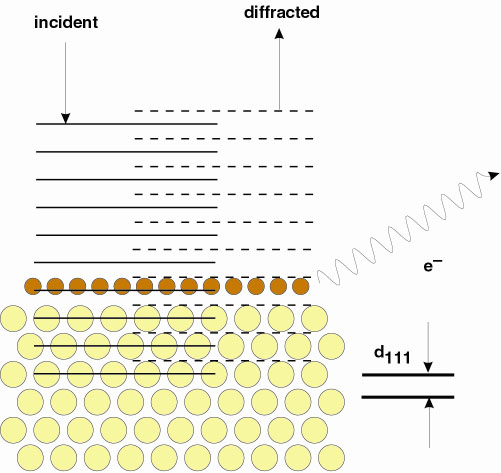 |
Fig. 60: Principle of the XSW technique using diffraction of a plane wave at |
We have investigated the impact of non-dipolar effects on XPS data with XSW. In contrast to the pure dipolar case, quadrupole contributions destroy the symmetric dipolar emission profile and can enhanced of the photoemission yield in the direction of the k-vector of the X-rays. Since an interference field is generated by the coherent superposition of two waves, i.e., an incident wave, travelling in one direction (i.e., k = kin) and a reflected wave (k = kout) travelling in another direction, this asymmetry can be determined easily. This is described in more detail in [1].
The results obtained at ID32 are shown in Figure 61 for a C- and O-containing molecular adsorbate (PTCDA) intentionally grown incoherently thick on Ag(111) [2]. At the Bragg reflection, the XPS signal (normalised to unity in the off-Bragg region) is enhanced compared to the (normalised) signal of the Auger electrons, which follows simply 1+R, where R is the reflectivity. The enhancement parameter SR of the XPS signal, which is about 1.8 for the present case, i.e., Y = 1 + SR R, directly reflects the quadrupole contributions and exemplifies the sensitivity of the XSW technique to the higher order terms in the scattering matrix element.
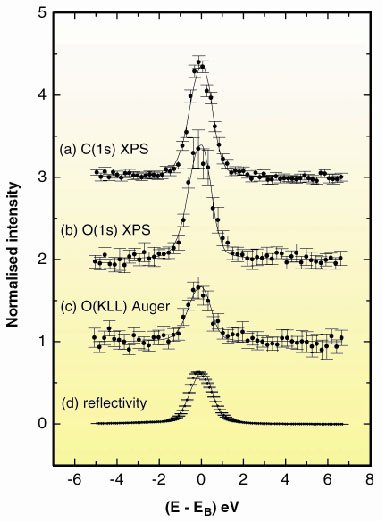 |
Fig. 61: Typical data for an incoherent layer containing oxygen and carbon as function of photon energy around the Bragg reflection. The enhancement of the XPS signals (a, b) compared to the Auger signal (c) in the region of the Bragg reflection is obvious. The Ag(111) reflectivity is shown in (d). |
A comparison of these parameters with quantum mechanical calculations is presently in progress. Obviously, the non-dipolar contributions can be significant, and their knowledge is crucial for a proper analysis of XSW and for high-energy X-ray photoemission data. In the present study, we only determined the amplitude of the multipole matrix element. Additionally, by employing the unique properties of XSWs with a defined phase relationship between incident and reflected wave, it is possible to determine both the amplitude and the phase of quadrupole contributions in the photoelectric scattering process, which have not been accessed at all with any other method. This is the subject of ongoing experiments.
References
[1] I.A. Vartanyants and J. Zegenhagen, Solid. State. Comm., 113, 299 (1999).
[2] F. Schreiber, K.A. Ritley, I.A. Vartanyants, H. Dosch, J. Zegenhagen and B.C.C. Cowie, Surf. Sci. Lett., 486, L519 (2001).
Principal Publication and Authors
F. Schreiber (a), K.A. Ritley (a), I.A. Vartanyants (a, b), H. Dosch (a), J. Zegenhagen (c) and B.C.C. Cowie (c), Surf. Sci. Lett., 486, L519 (2001).
(a) ITAP, Universität Stuttgart, and MPI-MF, Stuttgart (Germany)
(b) Institute of Crystallography RAS, Moscow (Russia)
(c) ESRF



