- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2001
- Materials
- Nucleation of Undercooled Liquid Metals
Nucleation of Undercooled Liquid Metals
Many liquids can be cooled, without observing solidification, far below their equilibrium melting temperature into a metastable undercooled liquid state. In the absence of external forces which may trigger the so-called heterogeneous nucleation process, the crystallisation of an undercooled liquid is driven by localised fluctuations in the configuration space, leading to the spontaneous formation of a stable crystalline nucleus (homogeneous nucleation) [1].
The crystallisation process of an undercooled drop can be schematised by the sequence of two steps: i) the appearance of a critical crystalline nucleus; ii) the propagation of the crystal front through the volume of the melt. In the case of liquid metals, the timescale to complete the transformation is largely dominated by the time required to form the crystalline nucleus.
The nucleation phenomenon can then be described by a physical quantity I defined as the number of crystallisation nuclei that are formed in the melt per second per volume (or mass) unit. This rate is strongly temperature dependent. The functional dependence of I(T) from fundamental quantities of undercooled liquids is illustrated by the standard theory of homogeneous nucleation. The study of nucleation phenomena and the experimental determination of I(T) are of crucial importance for the understanding of the physics of metastable liquids. In fact, I(T) is linked to basic thermodynamical quantities, and the nucleation phenomenon itself has critical implications in some metallurgical processes and in materials science.
We have developed a new experimental non-destructive method to measure I(T) in undercooled liquid metals. The method is based on the phase sensitivity of the X-ray absorption coefficient above core-electron absorption edges [2]. It can be applied to emulsions of liquid droplets or powder mixtures at high temperatures. By tuning the photon energy to a high solid-liquid contrast value, and during suitable sample temperature scans, one can accurately measure the liquid total mass fractions Xl(t) as a function of temperature (or time). Because of the intrinsic properties of the steady state nucleation process mechanism, once the Xl(t) are determined, it is possible to directly calculate the I(T) by a numerical solution of an appropriate integral equation. When compared with conventional one-particle techniques, the power of this new method relies on the fact that a large number of particles are probed simultaneously, thus largely improving the statistics of the measurement.
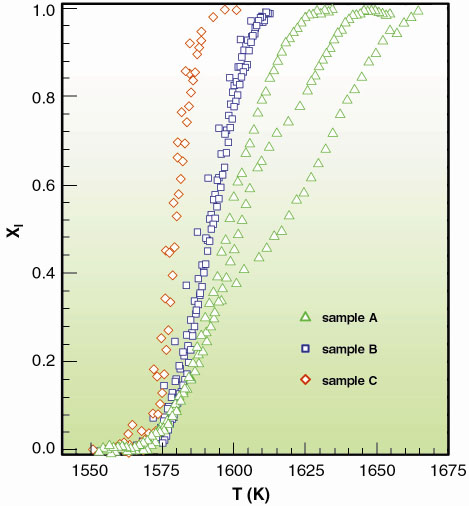 |
Fig. 113: Liquid fractions Xl[T(t)] curves as obtained from different X-ray absorption temperature scans. In each set of curves the cooling rate is larger when lower freezing temperatures are reached. |
As an example, we show how this method can be applied to the crystallisation of undercooled liquid palladium droplets dispersed in sintered Al2O3 powder. To measure I(T) over a wide temperature interval, we prepared three different samples A, B and C, characterised by substantially different Pd grain mass distribution. In Figure 113 we present the typical liquid fraction Xl[T(t)] curves measured by X-ray absorption temperature scans, at several cooling rates. The different slopes and limiting nucleation temperatures in the various curves have to be attributed to the spread in the cooling rates and to the differences in the size distributions among the three samples. The nucleation rate data obtained from those curves are reported in Figure 114, where we present the I(T) of undercooled liquid Pd spanning over about 6 orders of magnitude. By applying this method, one can obtain nucleation rates which are overlapping within the experimental errors, when starting from totally separated Xl(t) curves.
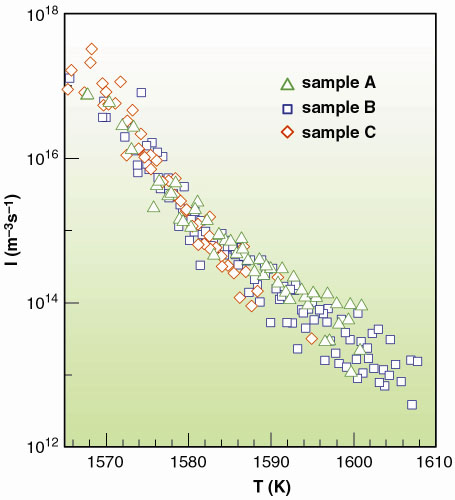 |
Fig. 114: Nucleation rate for undercooled liquid Pd in Al2O3 as determined by the new method described in this work. |
References
[1] P.B. Debenedetti, Metastable Liquids, Princeton University Press, Princeton, NJ (1994).
[2] A. Filipponi, M. Borowski, P.W. Loeffen, S. De Panfilis, A. Di Cicco, F. Sperandini, M. Minicucci and M. Giorgetti, J. Phys.: Condens. Matter 10, 235 (1998).
Principal Publication and Authors
S. De Panfilis (a) and A. Filipponi (b), J. Appl. Phys. 88, 562-570 (2000).
(a) UdR INFM and Dipartimento di Fisica, Camerino (Italy)
(b) UdR INFM and Dipartimento di Fisica, L'Aquila (Italy)



