- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2001
- Collective Atom Dynamics
- Optical Phonon Overbending in Diamond
Optical Phonon Overbending in Diamond
Despite the fact that diamond and silicon are neighbouring elements in the group IV of the periodical table, possessing the same crystal structure with tetrahedrally coordinated covalent bonds, their electronic band structure and lattice dynamics are profoundly different. For example, diamond is a perfect insulator of unparalleled hardness, while silicon is much softer and a semiconductor. One of the unusual properties of diamond, absent in silicon, which have intrigued scientists since its first observation in 1947, is the existence of a peak in the second order Raman spectra two times higher than the zone centre (-point) one phonon energy. Various explanations were put forward, but only the advent of reliable ab-initio computational methods allowed the reproduction of this unique feature. These calculations suggest that the peak is due to an "overbending" of the longitudinal optic (LO) phonon dispersion branches with a minimum at the
-point, and maxima reached at some arbitrary points along all three high-symmetry directions [1]. This prediction stimulated more detailed experimental work on this phonon mode, and an inelastic neutron scattering (INS) study, performed at the ILL, confirmed the overbending for the LO phonon branch along the
-direction ([1 0 0]) [2]. However, the results from a subsequent inelastic X-ray scattering (IXS) study are not in agreement quantitatively with the INS results, and furthermore the presence of overbending in the other directions was contested [3]. In order to resolve this controversy and apparent disagreement between the theoretical predictions and the IXS results, an accurate IXS study was performed on ID28.
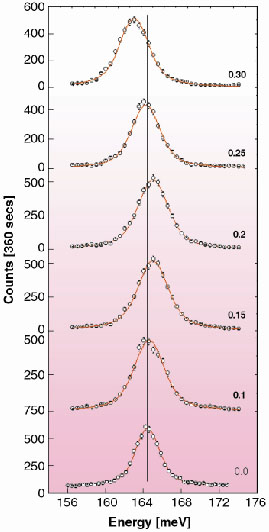 |
Fig. 77: Experimental IXS data (circles) and their best fits (solid lines) for the longitudinal optic phonon along |
The experiment was performed with a total energy resolution of 3 meV full-width-half-maximum (at 17794 eV incident energy). The diamond single crystal (4 mm diameter) was of excellent quality as testified by the narrow width of its rocking curve of only 0.004°. The stability and reproducibility of the instrument was checked by recording the Stokesanti-Stokes pair of a longitudinal acoustic phonon near the Brillouin zone centre, and by repeated scans of the -point phonon. Figure 77 shows representative spectra at reduced momentum transfer values, q, as indicated in the figure, obtained along the
-direction ([1 1 1]), together with their best fits to a Lorentzian profile. The data clearly reveal an overbending for 0.15 < q < 0.25. We furthermore note that the measured
-point phonon energy of 164.75 meV is in excellent agreement with Raman data, which yield 165.18 meV. Figure 78 shows the resulting dispersion relations for all three high-symmetry directions, together with the INS results and the ab initio calculations. The overbending, as determined by IXS, amounts to 1.5, 0.5 and 0.2 meV along the three high-symmetry directions (
,
and
). The IXS data are in very good agreement with both the INS results and the calculations. These results unambiguously reveal the LO overbending in all three high-symmetry directions, finally providing the physical origin for the anomalous peak in the two-phonon Raman spectrum. Furthermore, the present work demonstrates that the reproducibility of state-of-the-art IXS instruments, which is intimately linked to temperature stability of the high energy resolution optical components on the milli-Kelvin scale, can yield results reproducible within 10-3 on the time scale of weeks.
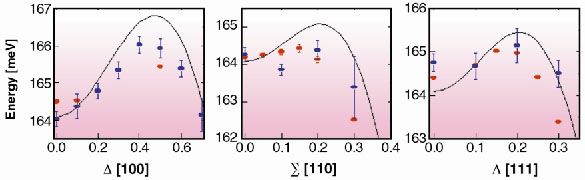 |
Fig. 78: Experimental (IXS: red points; INS: blue points) and calculated (solid lines) phonon dispersion relations along the three high-symmetry directions in diamond. |
References
[1] W. Windl, P. Pavone, K. Karch, O. Schutt, D. Strauch, P.Gianozzi and S. Baroni, Phys. Rev. B 48, 3164 (1993).
[2] J. Kulda, B. Dorner, B. Roessli, H. Sterner, R. Bauer, Th. May, K. Karch, P. Pavone and D. Strauch, Solid State Commun. 99, 799 (1996).
[3] M. Schwoerer-Bohning, A.T. Macrander and D.A. Arms, Phys. Rev. Lett. 80, 5572 (1998).
Principal Publication and Authors
J. Kulda (a), H. Kainzmaier (b), D. Strauch (b), B. Dorner (a), M. Lorenzen (c) and M. Krisch (c), submitted Phys. Rev. Lett.
(a) ILL
(b) Institut f. Theoretische Physik, Universität Regensburg (Germany)
(c) ESRF



