- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2000
- Surfaces and Interfaces
- Liquid-Vapour Interfaces at Short Length Scales
Liquid-Vapour Interfaces at Short Length Scales
Liquid-vapour interfaces, particularly those involving water, are common in both natural and artificial environments. They were first described, in 1893 by van der Waals, as regions of continuous variation of density caused by density fluctuations within the bulk phases (Figure 47). In contrast, the more recent capillary-wave model (1965) assumes a step-like density profile across the liquid-vapour interface, whose width is the result of the propagation of thermally excited capillary waves. The model has been validated for length scales of tens of micrometres and larger, but the structure of liquid surfaces on submicrometre length scales, where the capillary theory is expected to break down, remains poorly understood. One reason is that, in contrast to solid surfaces, the absence of relevant experimental information even for the simplest liquid-vapour interfaces precludes the assessment of any of the existing theories which considerably diverge in their conclusions.
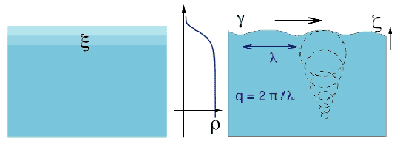 |
Fig. 47: The van der Waals description of a liquid-vapour interface (1893) predicts a smooth transition from the liquid density to the vapour density with a characteristic length related to the bulk correlation length. In the capillary wave model, the interface structure is due to the propagation of thermally excited capillary waves with wave-vector q. Their amplitude is inversely proportional to the surface tension or surface energy gamma.
|
Using grazing-incidence X-ray scattering, we have obtained the first complete determination of the free surface structure and of the wavevector-dependent surface energy for water and organic liquids. We observed a large decrease of the surface energy of sub-micrometer waves, which cannot be explained by the phenomenological capillary theories, and which is decisive in the long-standing dispute on structure of liquid interfaces.
The experiments were carried out at ID10B, the Troika 2 beamline. The liquid was contained in a large trough (330 mm in diameter) mounted on the diffractometer on an anti-vibration system. The atmosphere consisted of helium, in order to minimise background, saturated with the vapour of the liquid. The monochromatic 8 keV X-ray beam (0.3 mm x 0.2 mm, H x V) was first reflected by two mirrors for harmonic rejection, and then impinged on the surface with a grazing angle of incidence. To obtain surface sensitivity, it was adjusted to below the critical angle for total external reflection. We observed the scattering in the horizontal plane of the surface by using a vertically mounted gas-filled position sensitive detector. The experiment is analogous to a small-angle scattering experiment, however, with surface sensitivity provided by the scattering geometry. The data can be evaluated within the frame of the so-called distorted-wave Born approximation (DWBA) [1]. The Fourier modes of the liquid surface are capillary waves of wave vector q, which can be viewed as gratings diffracting the X-ray waves. The modes are thermally excited and their amplitude is inversely proportional to the effective surface energy or surface tension for wave vector q, which can therefore be determined from the scattering experiment (Figure 48). Compared to the predictions of phenomenological theories, we observe a lower surface tension at small wave vectors. This can be seen as a consequence of the non-locality of attractive intermolecular (van der Waals forces) as suggested by recent calculations [2]. Indeed, surface tension essentially arises due to missing neighbours and thus the lack of compensation for inter-molecular interactions at the surface. Therefore a reduction in surface energy or surface tension can be expected for a corrugated interface for wavelengths within the range of molecular interactions.
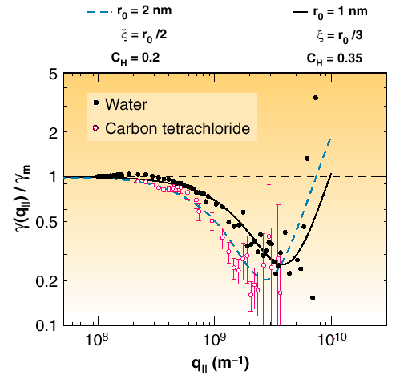 |
Fig. 48: (left) Scale-dependent surface tension obtained from the diffuse scattering experiments for water and carbon tetrachloride. The lines are calculated using the theory of Ref. [1] as described in text.
|
These results should have important implications for our understanding of all processes involving short-scale deformations of fluid interfaces and provide a stringent test for theories attempting to describe the structure of liquid interfaces.
References
[1] J. Daillant and A. Sentenac, "Diffuse scattering, in X-ray and Neutron Reflectivity, Principles and Applications, J. Daillant and A. Gibaud, eds, Springer-Verlag, Berlin Heidelberg (1999).
[2] K.R. Mecke and S. Dietrich, Phys. Rev. E, 59, 6766-84 (1999).
Principal Publication and Authors
C. Fradin (a), A. Braslau (a), D. Luzet (a), D. Smilgies (b), M. Alba (a), N. Boudet (b), K. Mecke (c) and J. Daillant (a,d), Nature 403, 871 (2000).
(a) CEA Saclay, Gif sur Yvette (France)
(b) ESRF
(c) Bergische Universität Wuppertal (Germany)
(d) LURE, Orsay (France)



