- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2000
- Soft Condensed Matter
- Capillary Waves in Slow Motion
Capillary Waves in Slow Motion
Surfaces of liquids are decorated with thermally activated capillary waves. Their amplitudes are on the order of angstroms. Many X-ray scattering experiments, which show the unambiguous fingerprints of capillary waves on liquid surfaces, have been performed in the past. These experiments, however, have tested the static time-averaged structure rather than the dynamics of the surface fluctuations. This is due to the major drawback that conventional X-ray sources are essentially incoherent, which renders the direct measurement of dynamics impossible. With high-brilliance third-generation sources it has become possible to obtain intense X-ray beams possessing a high degree of coherence. Such beams are produced by selecting the coherent part of the impinging radiation from an otherwise incoherent beam using micrometre-sized pinholes. These coherent beams make photon correlation spectroscopy with X-rays (XPCS) possible.
The first successful application of XPCS to monitor lateral motion at surfaces has been performed at ID10A, the Troïka beamline. The dynamics of capillary waves on the surface of the prototype glass former glycerol were measured as a function of temperature. The glycerol surfaces were illuminated with 8 keV X-rays under a grazing incident angle well below the critical angle of total reflection (Figure 34). Thus, the penetration depth of the radiation was restricted to the topmost few nanometres of the sample. The electron density contrast is very large at the surface compared with the liquid underneath. Hence, for incident angles below the critical angle, the scattering is dominated by contributions stemming from the surface rather than from the bulk.
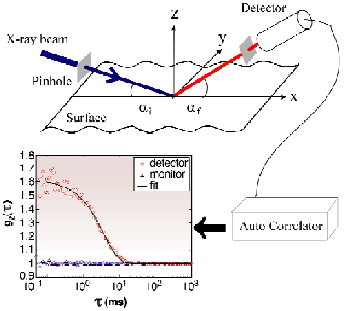 |
Fig. 34: Schematic layout of the experimental setup and example of a correlation function (inset).
|
The scattered radiation was detected under different exit angles within the scattering plane. Thereby, the lateral component qx of the wavevector transfer could be varied. From the qx-value the respective lateral length scale x0 = 2![]() /qx is easily obtained.
/qx is easily obtained.
Dynamics can be measured in a photon correlation spectroscopy experiment by evaluating the normalised time-correlation function g2(![]() ) = <I(t+
) = <I(t+![]() ) I(t)> / <I(t)>2 where I(t) is the observed intensity in a detector. We found that all of our data can be perfectly described by the exponential form g2(
) I(t)> / <I(t)>2 where I(t) is the observed intensity in a detector. We found that all of our data can be perfectly described by the exponential form g2(![]() ) = g0 exp(-
) = g0 exp(-![]() /
/![]() 2)+1 with 0
2)+1 with 0 ![]() g0
g0 ![]() 1 and a time constant
1 and a time constant ![]() 0. The constant g0 depends on the degree of coherence of the incident beam and the degree of ensemble averaging for the incident and scattered beam. The inset in figure 34 shows an example of a correlation function measured at T = 265.5 K for a lateral length scale x0 of 90 µm.
0. The constant g0 depends on the degree of coherence of the incident beam and the degree of ensemble averaging for the incident and scattered beam. The inset in figure 34 shows an example of a correlation function measured at T = 265.5 K for a lateral length scale x0 of 90 µm.
The observed time constants ![]() 0 as a function of the lateral length scale x0 are shown in Figure 35 for different temperatures T. A linear relationship between
0 as a function of the lateral length scale x0 are shown in Figure 35 for different temperatures T. A linear relationship between ![]() 0 and x0 is evident for all T. Figure 35 can be understood quantitatively by the capillary waves theory for viscous liquids [1,2]. For highly viscous liquids such as glycerol the damping of the surface waves is so large that all propagating modes become unstable. Thus, for high viscosities so-called overdamped capillary waves are expected. Their damping term
0 and x0 is evident for all T. Figure 35 can be understood quantitatively by the capillary waves theory for viscous liquids [1,2]. For highly viscous liquids such as glycerol the damping of the surface waves is so large that all propagating modes become unstable. Thus, for high viscosities so-called overdamped capillary waves are expected. Their damping term ![]() = 1/
= 1/![]() 0 is given by
0 is given by ![]() 0 = x0
0 = x0 ![]() (T) /
(T) / ![]()
![]() (T) where the dynamic viscosity
(T) where the dynamic viscosity ![]() (T) and the surface tension
(T) and the surface tension ![]() (T) are temperature-dependent quantities.
(T) are temperature-dependent quantities.
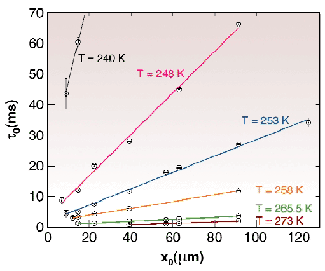 |
Fig. 35: Time constants as a function of the length of the capillary wave mode for different temperatures.
|
With our measurements we have covered a large temperature range in order to monitor in situ the freezing of the surface waves. Figure 35 directly reflects that the quasi long-ranged surface motion due to overdamped capillary waves starts to freeze on a time scale of seconds at temperatures of 230 K, i.e. far above the calorimetric glass transition temperature TG = 186 K.
References
[1] V.G. Levich, Physicochemical Hydrodynamics, Prentice-Hall, Englewood Cliffs NJ (1962).
[2] J. Jäckle and K. Kawasaki, J. Phys.: Condens. Matter 7, 4351 (1995).
Principal Publication and Authors
T. Seydel (a), A. Madsen (b), M. Tolan (a), G. Grübel (b), and W. Press (a), Physical Review B 63(7), (2001).
(a) University of Kiel (Germany)
(b) ESRF



