- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2015
- Electronic structure, magnetism and dynamics
- The core of the Moon revealed by synchrotron experiments
The core of the Moon revealed by synchrotron experiments
Sound velocity and density measurements carried out on iron at pressure and temperature conditions expected at the centre of the Moon have been used to reinterpret seismic records obtained at the time of the Apollo space programme and to propose a structural, compositional and velocity model of the Moon’s metallic core.
Iron (Fe) is the main component of the core of telluric planets (those with an overall layered structure similar to that of Earth). Fe adopts a hexagonal close packed structure (hcp or ε phase) under pressure (P) and temperature (T) conditions of the Earth’s inner core, whereas a face-centred cubic structure (fcc or γ phase) is expected under the more moderate P-T characteristic of the cores of smaller planetary bodies, such as the Moon, Mercury and Mars. Accordingly, the knowledge of the physical properties of the different iron phases at pertinent thermodynamic conditions is essential to model planetary cores. Above all, density and sound velocities are of primary importance for the proper interpretation of the seismological data and ultimately to produce accurate planetary models.
The Moon is the only other planetary body beside the Earth for which multiple direct seismic observations are available. The Apollo Lunar Surface Experiments Package has provided very precious information on the Moon’s interior. However, seismic investigations of the deepest lunar interior (> 900 km depth) remain challenging. In particular, the structure of the core is controversial, with only a single seismic study that directly detects the existence of a solid inner and a fluid outer core [1]. However, a complete and consistent set of measurements of compressional and shear wave sound velocities (respectively, VP and VS) and density (ρ) at high pressure and high temperature for γ-Fe was absent. Therefore, our understanding was based on untested assumptions on the physical properties of iron and iron alloys at relevant P-T conditions.
In this study, we have carried out density and sound velocity measurements on both body-centred cubic (bcc) and fcc iron between 0 GPa and 19 GPa and 300 K and 1150 K, using inelastic X-ray scattering (IXS) combined with X-ray diffraction (XRD) measurements at beamline ID28. IXS allows a clear identification of longitudinal aggregate excitations in polycrystalline samples, the direct derivation of VP, and the estimation of VS. This technique has been proven very suitable for measurements on metallic samples compressed in diamond anvil cell under simultaneous high P−T conditions [2]. Furthermore, combined XRD measurements yield an unambiguous phase determination and the direct derivation of the sample density.
 |
|
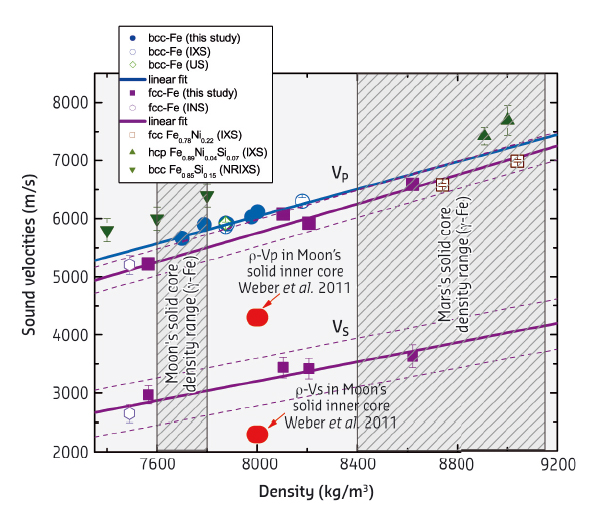
Fig. 56: Density evolution of the aggregate compressional and shear sound velocities of pure-Fe and selected Fe-alloys. The arrows point to VP−ρ and VS−ρ values proposed in [1] for the Moon’s solid core. |
The results obtained are displayed in Figure 56. Both bcc and fcc phases show a linear VP−ρ relationship over the investigated P-T range. The sound velocity of the fcc phase is about 400 m/s lower than that of the bcc phase at the same density. Most importantly, the VP value proposed for the Moon’s inner core [1] after a reanalysis of Apollo lunar seismograms is significantly below those of γ-Fe. Such a large difference is hardly explainable even when considering anharmonic effects at higher temperatures, frequency-dependent viscoelastic relaxations, or effects of alloying with nickel or other plausible light elements.
 |
|
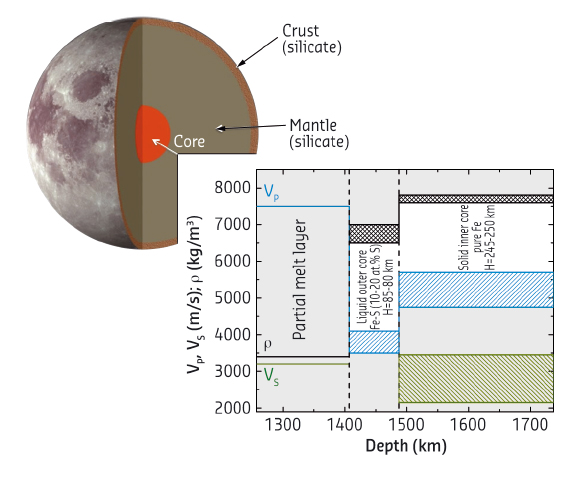
Fig. 57: Schematic view of the interior of the Moon and a close-up of the proposed core model. |
Nonetheless, seismic data analysis and refinements of the lunar moment of inertia require the Moon to have a solid inner core and a liquid outer core. We then use our experimental results to construct a direct lunar core model, reinterpreting the seismic observations on the basis of our measurements. The resulting velocity and density model is shown in Figure 57. We put forward a solid inner core, made of pure-Fe, having a radius of ∼245–250 km, surrounded by a sulfur-bearing (6-11 wt%) liquid outer core ∼85–80 km thick. We further validated our model by comparison with Moon observables such as mass and moment of inertia, finding values that fall within 0.1% of known values.
Principal publication and authors
Toward a mineral physics reference model for the Moon’s core, D. Antonangeli (a), G. Morard (a), N.C. Schmerr (b), T. Komabayashi (c), M. Krisch (d), G. Fiquet (a) and Y. Fei (e), Proc. Natl. Acad. Sci. USA 112, 3916 (2015); doi: 10.1073/pnas.1417490112.
(a) Institut de Minéralogie, de Physique des Matériaux, et de Cosmochimie (IMPMC), UMR CNRS 7590, Sorbonne Universités – UPMC, Muséum National d’Histoire Naturelle, IRD Unité 206, Paris (France)
(b) Department of Geology, University of Maryland, College Park MD (USA)
(c) Department of Earth and Planetary Sciences, Tokyo Institute of Technology (Japan)
(d) ESRF
(e) Geophysical Laboratory, Carnegie Institution of Washington, Washington DC (USA)
References
[1] R.C. Weber et al., Science 331, 309 (2011).
[2] D. Antonangeli et al., Earth Planet. Sci. Lett. 331, 210 (2012).



