- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2014
- Electronic structure and magnetism
- CaIrO3: a spin-orbit Mott insulator beyond the jeff = 1/2 ground state
CaIrO3: a spin-orbit Mott insulator beyond the jeff = 1/2 ground state
Spin-orbit coupling, when compared to the energy scale of other interactions, is usually neglected in the description of correlated 3d transition metal compounds. However, in compounds containing 5d elements its role grows in importance and the combined influence of electron correlation and spin-orbit coupling gives rise to novel quantum phases and transitions.
The insulating behaviour of antiferromagnetic Sr2IrO4, for example, is unexpected for a system with a half-filled outermost electronic shell and spatially extended orbitals. The conventional Mott mechanism often invoked to explain the insulating character of strongly correlated systems cannot be envisaged here as electron correlation is small. However, in combination with a strong cubic crystal field, spin-orbit coupling enhances the effect of electronic correlation through the formation of the so-called jeff = 1/2 ground state: Sr2IrO4 was therefore termed a spin-orbit Mott insulator [1].
Whether this scenario also holds true for CaIrO3 is debatable because sizeable octahedral distortions are expected to drastically lower the symmetry of the crystal field compared to Sr2IrO4. The robustness of the jeff = 1/2 ground state against structural distortions has been mostly tested by means of resonant X-ray magnetic scattering. However, the interpretation of RXMS has been strongly debated and, in the specific case of CaIrO3, a unified picture of the ground state has not yet been reached: in fact, the interpretation of experimental results [2] has been contradicted by theoretical calculations [3].
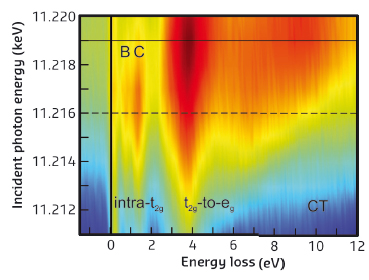
We used resonant inelastic X-ray scattering (RIXS) at the Ir L3 edge to address the problem of the electronic structure of CaIrO3. RIXS measurements were carried out at ID20, the new inelastic X-ray scattering beamline. Figure 9 shows a RIXS map of CaIrO3. An elastic line, magnetic excitations and possibly phonons are found close to the zero energy loss line. At increasing energy losses, we assign features to intra-t2g (5d t2g5 → 5d t2g5), t2g-to-eg (5d t2g5→ 5d t2g4eg1) and charge-transfer (CT) excitations, following previous RIXS studies. In this work, we focus on intra-t2g excitations only, i.e. excitations in which electrons are promoted within the 5d t2g manifold. These are composed by two peaks at 0.65 (B) and 1.22 eV (C), respectively.
 |
|
Fig. 9: Ir L3 edge RIXS map of CaIrO3. |
To better understand the nature of these excitations and to estimate the effective tetragonal contribution to the crystal field splitting and spin-orbit coupling in CaIrO3, we adopted a single-ion model [4]: the interacting Hamiltonian for one hole in the 5d t2g states is then written as H = ξL⋅S - ΔLz2, in which the tetragonal crystal field splitting Δ and spin-orbit coupling ξ are treated on equal footing. The transition energies are reproduced for ξ = 0.52 and Δ = –0.71 eV. The sign of Δ is consistent with structural studies reporting a compression of the IrO6 octahedrons and implies a minor contribution of the xy orbital to the ground state wave function (only 10%). We conclude that the wave function of CaIrO3 differs significantly from that of Sr2IrO4, for which xy, yz and zx orbitals are equally occupied.
 |
|
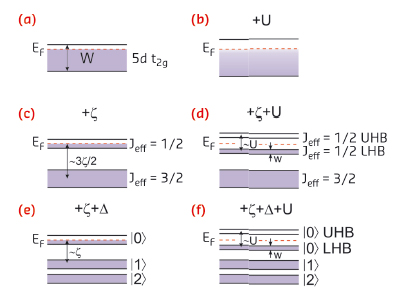
Fig. 10: Schematic band structure of 5d5 iridates in the absence of perturbations (a), with spin-orbit coupling (c), and spin-orbit coupling plus tetragonal crystal field splitting (e). Panels (b), (d), and (f) correspond to panels (a), (c) and (e), respectively, when the Hubbard term U is taken into account. |
How to explain the insulating behaviour for CaIrO3 then? Consider the whole 5d t2g manifold (Figure 10a): the bandwidth W would be too large for a reasonable Hubbard energy U (<W) to open a gap; rather, the density of states at the Fermi energy would only be slightly reduced (Figure 10b). Crucially, spin-orbit coupling splits the otherwise degenerate 5d t2g states and a half filled jeff = 1/2 band is isolated, with a bandwidth w < W (Figure 10c). As now U > w, a lower (LHB) and an upper (UHB) Hubbard band are created, and the system turns into an insulator (Figure 10d): this is the mechanism introduced to explain the insulating behaviour of Sr2IrO4. In CaIrO3, however, the tetragonal crystal field is comparable to the spin-orbit coupling and three Kramers doublets are formed (Figure 10e). Finally, however, the action of U is similar to the pure jeff = 1/2 case in view of the similar narrowing of the conduction band (Figure 10f). Therefore, we conclude that CaIrO3 can also be classified as a spin-orbit Mott insulator.
Principal publication and authors
M. Moretti Sala (a), K. Ohgushi (b), A. Al-Zein (a), Y. Hirata (b), G. Monaco (a,c) and M. Krisch (a), Phys. Rev. Lett. 112, 176402 (2014).
(a) ESRF
(b) Institute for Solid State Physics, University of Tokyo, Kashiwa (Japan)
(c) Dipartimento di Fisica, Università di Trento, Povo (Italy)
References
[1] B.J. Kim et al., Phys. Rev. Lett. 101, 076402 (2008).
[2] K. Ohgushi et al., Phys. Rev. Lett. 110, 217212 (2013).
[3] N.A. Bogdanov et al., Phys. Rev. B 85, 235147 (2012).
[4] M. Moretti-Sala et al., Phys. Rev. Lett. 112, 026403 (2014).



