- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2014
- Electronic structure and magnetism
- Measuring the Dzyaloshinskii–Moriya interaction in a weak ferromagnet
Measuring the Dzyaloshinskii–Moriya interaction in a weak ferromagnet
The Dzyaloshinskii–Moriya interaction (DMI) plays a crucial role in several of the most topical phenomena in magnetism, including the slow magnetic rotation found in skyrmion lattices and cycloidal magnetoelectrics. The original formulation of the DMI related to the occurrence of ‘weak ferromagnetism’ in nominally collinear antiferromagnetic materials such as aFe2O3, MnCO3 and FeBO3 [1,2]. Unfortunately, in these archetypal twisted magnetic systems, the sign of the DM interaction has eluded experimenters because it affects only the phase of magnetic scattering, whereas experiments based on a single scattering mechanism determine only intensity (a manifestation of the famous ‘phase problem’ of crystallography). This meant that the DMI in such weak ferromagnets could be determined in magnitude and axial direction, but not in sign.
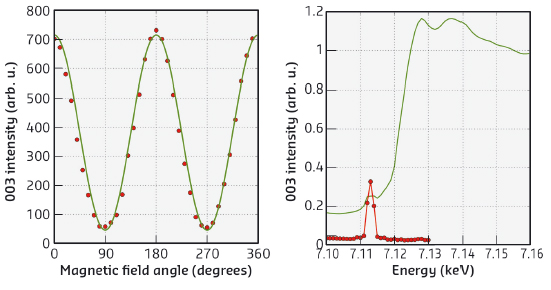
Following the suggestion that the sign of the DMI might be determined by measuring interference between non-resonant magnetic X-ray scattering and the pure quadrupole resonance at the K absorption edge [3], magnetic and resonant quadruple scattering were first investigated separately on a sample of FeBO3 (Figure 6). The magnetic structure was observed in the conventional way, by rotating the magnetism with respect to the X-ray probe. However, with this class of weak ferromagnets we were able to carry out such a rotation with a static crystal, using a small rotating magnet to turn the entire magnetic structure. This approach allows very high-quality data to be obtained from a rapid series of measurements. The quadrupole resonance can be seen very clearly as a sharp peak in the pre-edge region (Figure 6).
 |
|
Fig. 6: Spacegroup-forbidden diffraction intensities arising from pure non-resonant magnetic scattering (left) and pure quadrupole resonant scattering (right – red line) as a function of photon field angle and energy, respectively. |
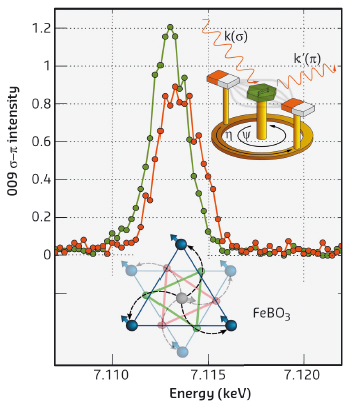
The final step was to create the conditions whereby these two scattering processes occur simultaneously and can interfere with each other. To this end, measurements of the (009) resonant quadrupole reflection were carried out at BM28, again rotating the magnet to manipulate the antiferromagnetic structure, causing the phase of the magnetic scattering to be reversed. This produced a remarkable jump in the energy of the resonance due to the reversal of the interference conditions on the low and high energy side of the peak (Figure 7). From the direction of the jump, we were able to determine the phase of the magnetic scattering and finally the sign of the DMI.
 |
|
Fig. 7: The jump in the quadrupole resonance as the magnetic structure was rotated by 180 degrees. The relationship between the twisting of the magnetic moments and that of triangles of oxygen atoms between the iron planes is shown at the bottom. |
Armed with these results, we could provide a thorough test of state-of-the-art first-principles calculations. A realistic simulation of the spin canting in antiferromagnets leading to weak ferromagnetism requires an accurate account of the spin-orbit coupling, Coulomb correlations and hybridisation of the atomic states. To solve this problem we have developed a method for calculating the DMI based on the local force theorem, by considering the change in energy with respect to the twisting of the magnetic moments away from collinear ordering, Dij = δE/δΦij. We proposed [4] a new nonlocal inter-site formulation of the DMI,
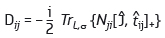
where Nji is the inter-site occupation matrix, J is the total moment operator, tij is the hopping matrix and [.,.]+ represents an anticommutator. Our method leads to a compact and transparent form that can take into account hybridisation, correlation and temperature effects in the system. Moreover, it can be applied to a wide range of the materials with different strengths of the spin-orbit coupling and Coulomb correlations.
The calculations of the isotropic exchange and DMI by this method have shown that weak ferromagnetism in FeBO3 is fully described by the six exchange interactions between atoms belonging to the first coordination sphere. Crystal symmetry dictates that the net DMI is along the c axis, which means that there is weak ferromagnetism in the ab plane. Both the sign and magnitude of the small twisting of the spins from collinear ordering are in excellent agreement with experimental data.
In conclusion, we have applied a novel experimental technique to a classic problem – the origin of weak ferromagnetism in FeBO3 – and shown that the results are in excellent agreement with a new theoretical method that can be used to model the Dzyaloshinskii-Moriya interaction in a wide range of materials.
Principal publication and authors
V.E. Dmitrienko (a), E.N. Ovchinnikova (b), S.P. Collins (c), G. Nisbet (c), G. Beutier (d), Y.O. Kvashnin (e), V.V. Mazurenko (f), A.I. Lichtenstein (g) and M.I. Katsnelson (f,h), Nature Physics 10, 202–206 (2014).
(a) A.V. Shubnikov Institute of Crystallography RAS, Moscow (Russia)
(b) Faculty of Physics, M.V. Lomonosov Moscow State University (Russia)
(c) Diamond Light Source Ltd, Didcot (UK)
(d) SIMaP, CNRS, Grenoble-INP & UJF, Saint-Martin d’Hères (France)
(e) ESRF
(f) Department of Theoretical Physics and Applied Mathematics, Ural Federal University, Ekaterinburg (Russia)
(g) I. Institut für Theoretische Physik, Universität Hamburg (Germany) (h) Institute for Molecules and Materials, Radboud University Nijmegen (The Netherlands)
References
[1] I. Dzyaloshinsky J. Chem. Phys. Solids 4, 241-255 (1958).
[2] T. Moriya Phys. Rev. 120, 91–98 (1960).
[3] V.E. Dmitrienko et al., JETP Lett. 92, 383–387 (2010).
[4] M.I. Katsnelson, Y.O. Kvashnin, V.V. Mazurenko and A.I. Lichtenstein Phys. Rev. B 82, 100403 (2010).



