- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2011
- Soft condensed matter
- Complex patterns in liquid crystals
Complex patterns in liquid crystals
A new way of making small molecules self-assemble into highly complex nanopatterns has been established that will help expand the capabilities of nanopatterning for advanced functional materials. Liquid crystals can form many diverse nanoscale structures. Particularly intriguing are the new liquid crystals honeycombs formed by T- or X-shaped molecules composed of several mutually incompatible rigid and flexible parts. A bee honeycomb can be represented in 2D as a tiling of hexagonal tiles. Here we show how in liquid crystals the tiles can be of many different shapes and colours, forming periodic patterns of high complexity.
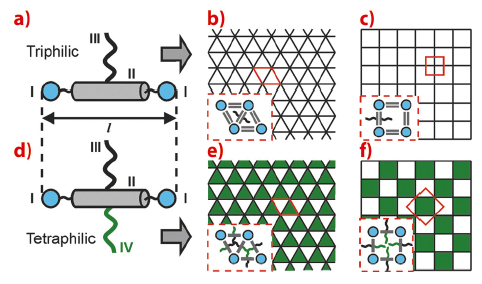
T-shaped molecules consisting of a rigid rod aromatic core (II in Figure 52a) capped at each end with hydrogen-bonding groups like glycerol (I) and having a flexible non-polar side chain, such as alkyl (III), have been found to assemble in honeycombs with cells of different polygonal cross-sections [1]. The rods, lying perpendicular to the channel axis, form the cell walls (“wax”), while the side-chains (“honey”) fill the cells. The larger the side-chain, the more sides to the polygon; thus compounds with small chains form triangular cells (Figure 52b), those with longer chains form square cells (Figure 52c), through pentagonal, hexagonal and beyond. If, however, a second chain (IV) is attached to the opposite side of the rod, an X-shaped molecule results (Figure 52d). If, moreover, that second chain is incompatible with the first one, we could obtain honeycombs described as two-colour tilings. Two examples are shown in Figures 52e,f. Even more elaborate tilings can also be conceived [2].
If the chain volumes are too large for triangular yet too small for square cells then regular structure formation can be highly frustrated. Utilising such geometric and incompatibility frustration, compounds were synthesised giving a range of liquid crystal honeycombs with highly complex self-assembled “multicolour tiling” patterns. well-aligned thin films of X-shaped liquid crystals on silicon surface were studied using grazing incidence small-angle X-ray scattering (GISAXS) on beamline BM28 (XMaS).
 |
|
Fig. 52: b,c) Schematics of “single-colour” liquid crystal honeycombs formed by T-shaped “triphilic” molecules (a). e,f) “Two-colour” honeycombs formed by X-shaped “tetraphiles” (d). |
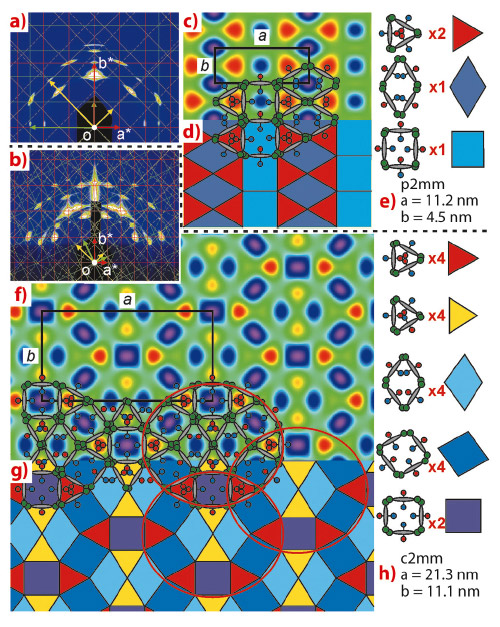
Figures 53a and b show GISAXS patterns of two honeycomb phases of a compound with a perfluoroalkyl and a carbosilane side-chain. Superimposed on the GISAXS patterns are the corresponding 2D reciprocal lattices in several orientations. Although the molecules are small (ca 4 nm), the unit cells are large: 21 x 11 nm for the high-temperature phase. By Fourier analysis, electron density maps were constructed (Figures 53c,f). To explain the maps, schematic molecules are superposed, bearing in mind that the perfluoro-chains have the highest electron density (blue-purple) and the carbosilane the lowest (red). It emerges that in neither of the two phases is there a clean separation between the two types of chains possible. The optimum compromise achieved by the liquid crystal in the low-temperature phase is a honeycomb composed of pure carbosilane triangles (red, Figure 53e), pure fluoroalkyl rhombuses (dark blue), and squares in which the two chains are mixed (light blue).
 |
|
Fig. 53: a,b) GISAXS patterns of a thin film of an X-shaped liquid crystal compound in the low- and high-temperature phases. c,f) Corresponding electron density maps (purple high, red low), with schematic molecules partly superposed (red and green side-groups are carbosilane and perfluoroalkyl chains). d,g) Representation of the honeycombs as tilings. e,h) Tile types constituting the two phases and their number in a unit cell. |
Even more complex is the high-temperature phase. This honeycomb contains eighteen channels in a unit cell. They are of five different colours (compositions) and four different shapes, shown in Figure 53h. These structures show the remarkable ability of liquid crystals to find the optimum solution to the problem of geometric and compositional frustration, and the overriding tendency to form periodic structures. Even so, occasionally there may come a point when the unit cell becomes so large that the system gives up on periodicity and opts for an aperiodic solution. This still does not mean giving up on long-range order. Long-range positional order without periodicity was inconceivable until 1980s, when this year’s Nobel laureate Dan Shechtman discovered quasicrystals in metal alloys. This intriguing and mind-boggling condensed state was recently also discovered in liquid crystals. The tiling pattern in Figure 53g shows features hinting that a “forbidden” dodecagonal quasicrystalline honeycomb may be round the corner – see the red ellipses in Figure 53g. Preliminary results of research in this direction are encouraging.
Principal publication and authors
X.B. Zeng (a), G. Ungar (a), C. Tschierske (b), R. Kieffer (b), B. Glettner (b), F. Liu (a), C. Nürnberger (b), K. Pelz (b), M. Prehm (b), U. Baumeister (b), H. Hahn (c), H. Lang (b), G.A. Gehring (a), C.H.M. Weber (a) and J.K. Hobbs (a), Science 331, 1302 (2011).
(a) University of Sheffield, Sheffield (U.K.)
(b) Martin-Luther-University Halle-Wittenberg, Halle (Germany)
(c) TU Chemnitz, Chemnitz (Germany)
References
[1] G. Ungar, C. Tschierske, V. Abetz, R. Holyst, M. A. Bates, F. Liu, M. Prehm, R. Kieffer, X.B. Zeng, M. Walker, B. Glettner and A. Zywocinski, Adv. Funct. Mater. 21, 1296 (2011).
[2] B. Glettner, F. Liu, X.B. Zeng, M. Prehm, U. Baumeister, M.A. Bates, M. Walker, P. Boesecke, G. Ungar and C. Tschierske, Angew. Chem. Int. Ed. 47, 9063 (2008).



