- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2011
- Dynamics and extreme conditions
- Equivalence of the boson peak in glasses to the transverse acoustic van Hove singularity in crystals
Equivalence of the boson peak in glasses to the transverse acoustic van Hove singularity in crystals
Glasses are remarkably different from crystals at low temperature. They accumulate more heat and conduct less. This anomaly is related to a particular ensemble of atomic motions called the “boson peak”, whose nature has remained unknown for more than 50 years.
Before the 1960s, a glass was thought to be an ideal elastic medium, where atomic motions are determined by sound waves according to the Debye model. According to C. Kittel’s textbook, “the point was so obvious that it did not encourage experimental investigation”. Measurements of specific heat and thermal conductivity, however, revealed strong deviations from the Debye behaviour. A little later these deviations were attributed to the boson peak – a universal feature in the density of vibrational states (DOS) for all glasses. Since then, the vibrations of atoms in glasses have remained a point of controversy. Dozens of theoretical models and hundreds of experimental results did not provide a unified picture of how disorder in atomic positions makes glasses thermodynamically so different from ordered crystals. Driven by the distinction from crystalline properties, the majority of theoretical models explained the boson peak by embracing features beyond sound waves. However, recent studies conducted on beamlines ID18, ID27, and ID28 shows that this is not the case.
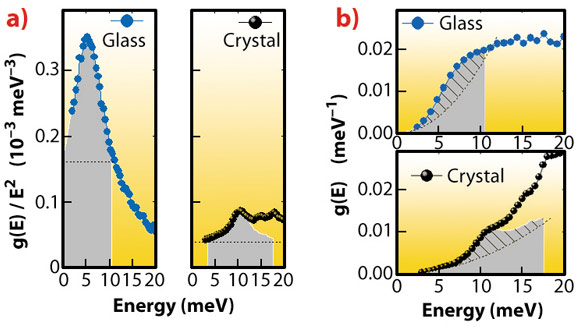
In this work, the atomic motions in a glass and a crystal were compared using nuclear inelastic scattering, a technique that determines the exact number of vibrational states. The results show that around the boson peak, the number of states in a glass is exactly the same as the number of sound wave states in the crystal around the transverse acoustic (TA) van Hove singularity (Figure 5). Thus, the glass has no additional modes in excess of the sound waves in the crystal.
 |
|
Fig. 5: Comparison of atomic vibrations in the sodium silicate glass and in the corresponding crystal. There is an apparent excess of states in the glass relative to the crystal in the reduced DOS g(E)/E2 (panel a), but the number of states is the same (panel b). The filled areas of the DOS in (b) correspond to the filled areas of the reduced DOS in (a) within the FWHM of the boson peak (in the glass) and of the TA singularity peak (in the crystal), respectively. The dashed lines show the Debye levels. The hatched parts of the filled areas mark the excess of states over the Debye level. |
The equivalence of the boson peak and the TA singularity in the absolute number of states suggests that the vibrational states of the boson peak belong to acoustic branches. Indeed, an alternative attribution of the boson peak to additional modes would face a problem to explain the ~35% deficit of acoustic states in the glass.
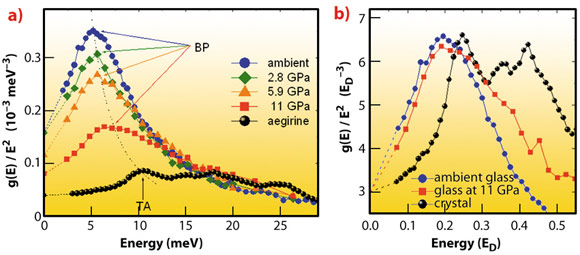
Application of pressure causes the transformation of the reduced DOS of the glass towards the reduced DOS of the crystal: the boson peak decreases in height and shifts to higher energy, moving towards the TA singularity (Figure 6a). Measurements of density and sound velocity suggest that the transformation is caused by a gradual stiffening of the elastic medium. Once corrected for the difference in the elastic medium (re-plotted in the Debye energy (ED) units), the boson peak matches the transverse acoustic singularity in height and energy (Figure 6b).
 |
|
Fig. 6: a) With increasing pressure the boson peak (BP) moves towards the transverse acoustic (TA) singularity of the crystal. b) Once corrected for the difference in the elastic medium, the boson peak matches the TA singularity in height and energy. |
These observations unambiguously identify the boson peak with sound waves. They lead to the conclusion that the anomaly in the heat capacity of glasses arises not from additional modes, but from sound waves, which have, however, lower frequencies in glasses due to structural disorder. Unexpectedly, but in accordance with the general theory of knowledge, the sound-wave nature of glass anomalies revealed here is a return to the earliest ideas, but with a new level of understanding.
Principal publication and authors
A.I. Chumakov (a), G. Monaco (a), A. Monaco (a), W.A. Crichton (a), A. Bosak (a), R. Rüffer (a), A. Meyer (b), F. Kargl (b), L. Comez (c), D. Fioretto (c,d), H. Giefers (e), S. Roitsch (e), G. Wortmann (e), M.H. Manghnani (f), A. Hushur (f), Q. Williams (g), J. Balogh (e), K. Parlinski (h), P. Jochym (h) and P. Piekarz (h), Physical Review Letters 106, 225501 (2011).
(a) ESRF
(b) Technical University of Munich (Germany)
(c) University of Perugia (Italy)
(d) University of Rome (Italy)
(e) University of Paderborn (Germany)
(f) University of Hawaii (USA)
(g) University of California at Santa Cruz (USA)
(h) Institute of Nuclear Physics, Krakow (Poland)
References
[1] R.H. Dicke, Phys. Rev. 93, 99 (1954).
[2] R. Friedberg, S.R. Hartmann, and J.T. Manassah, Phys. Rep. C 7, 101 (1973).



