- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2007
- Materials Science
- Solving the structure of the binary icosahedral Yb-Cd quasicrystal
Solving the structure of the binary icosahedral Yb-Cd quasicrystal
Where are the atoms? This question has been puzzling scientists ever since the discovery of quasicrystals some 25 years ago by Shechtman and coworkers [1]. Quasicrystals are extremely well ordered structures whose atomic arrangement is non periodic. This shows up in their diffraction patterns which display sharp Bragg reflections (a signature of long-range order) but with a 5-fold rotational symmetry, incompatible with lattice translation. This prevents the application of standard crystallography techniques to solve the structure. A high dimensional crystallographic approach has been developed, in a way similar to that achieved for incommensurately modulated structures. In this approach, periodicity is recovered in a 6 dimensional space, allowing modelling and a comparison with experimental data.
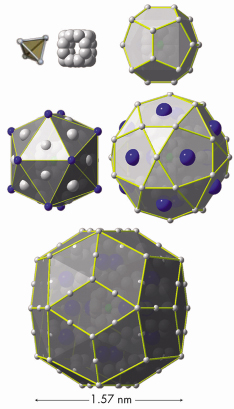
The discovery of the icosahedral phase of Cd5.7Yb by Tsai and coworkers [2] has been a breakthrough. Indeed, all previously known stable quasicrystals were at least ternary compounds. The dicovery that the CdYb quasicrystal is binary makes the structural analysis much simpler. There is also good scattering contrast for X-rays between the Cd and Yb atoms. Finally, there are two so-called periodic approximants, which can be synthesised with chemical compositions very close to that of the quasicrystal. The structure of the approximant crystals could be solved using standard crystallographic techniques and is described by a periodic packing of a large structural unit with an icosahedral symmetry, whose external shell is a triacontahedron (Figure 47). Starting from the centre, there is a Cd tetrahedron, occurring with different orientations, enclosed in a Cd dodecahedron. Then comes an Yb icosahedron (blue colour atoms) enclosed in two following shells containing Cd atoms only. This large triacontahedral atomic cluster has a diameter of 1.57 nm and is extremely well ordered chemically. Clusters are densely packed and connected along their 2-fold axes where they share a face and along 3-fold axes where they interpenetrate. The same cluster and connectivity rule has been used to model the quasicrystal, but on a quasiperiodic network.
 |
|
Fig. 47: Illustration of the shell structure of the cluster which appears in both the periodic approximant and the icosahedral quasicrystal. The external cluster has a diameter of 1.57 nm and contains 158 atoms. |
The structure of the icosahedral CdYb quasicrystal has been solved using a set of Bragg intensities collected at BM02, the D2AM CRG beamline. A large number of independent reflections has been measured in a large Q range, and with special care for weak reflections which are crucial for detailed modelling. Using a 6-dimensional analysis including a phase reconstruction procedure and the information obtained from the approximant structure, a model could be proposed which has been refined against the experimental data. The 5000 measured Bragg intensities impose a severe constraint on the modelling, which results in a very good R factor equal to 0.11. We find that the CdYb quasicrystalline structure is described by a quasiperiodic packing of the triacontahedral cluster, with connections along 2- and 3- fold axes as observed in the approximant: 94% of the atoms belong to such clusters.
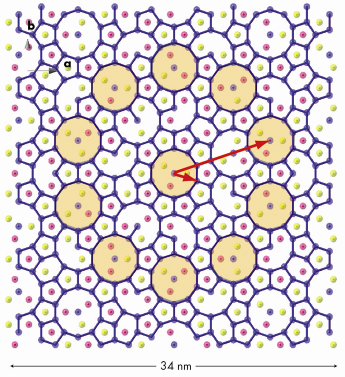
The model also leads to a hierarchical packing of the clusters, illustrated in Figure 48 which shows the cluster centre distribution in a 5-fold plane. Blue colour dots stand for cluster centres in the plane, whereas other colours stand for cluster centres lying below or above the plane. The solid lines are the 2-fold connections with a length equal to 1.57 nm. The clusters are packed together to form a ‘cluster of clusters’ whose trace is a 10-fold ring highlighted by a pale orange disk in Figure 48. In turn this ‘cluster of clusters’ which has an inner radius of about 2.5 nm also forms a larger cluster whose characteristic length is 10.7 nm, i.e. ![]() 3 larger, where
3 larger, where ![]() = 1.6168 is the golden mean (red arrows). This inflation property continues to infinity and might be used to explain some of the quasicrystal’s physical properties.
= 1.6168 is the golden mean (red arrows). This inflation property continues to infinity and might be used to explain some of the quasicrystal’s physical properties.
 |
|
Fig. 48: Illustration of inflation properties in the quasicrystal. The distribution of cluster centres (blue dots) is shown in a 5-fold plane. The pale orange disk is a trace of a cluster of clusters forming a 10-fold ring. In turn this cluster of cluster forms a self similar larger unit as highlighted by the long red arrow. |
Now that we have located the atoms in this icosahedral quasicrystal, detailed simulations can be performed to gain a deeper understanding of the physical properties and to tackle the still open and fascinating question of why the long range quasiperiodic order sets in.
References
[1] D. Shechtman, I. Blech, D. Gratias and J.W. Cahn, Phys. Rev. Lett. 53, 1951 (1984).
[2] A.P. Tsai, J.Q. Guo, E. Abe, H. Takakura and T.J. Sato, Nature 408, 537 (2000).
Principal publication and authors
H. Takakura (a), C.P. Gómez (b), A. Yamamoto (c), M. de Boissieu (d), A.P. Tsai (b), Nature Materials 6, 58-63 (2007).
(a) Division of Applied Physics, Graduate School of Engineering, Hokkaido University, Sapporo (Japan)
(b) Institute of Multidisciplinary Research for Advanced Materials, Tohoku University, Sendai (Japan)
(c) Advanced Materials Laboratory, NIMS, Tsukuba (Japan)
(d) Laboratoire de Thermodynamique et de Physico-Chimie Métallurgique, UMR CNRS 5614, ENSEEG-INPG, Saint Martin d’Hères (France)



