- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2003
- X-ray Absorption and Magnetic Scattering
- Dynamics of Long-wavelength Phason Fluctuations in the Icosahedral Quasicrystal i-AlPdMn
Dynamics of Long-wavelength Phason Fluctuations in the Icosahedral Quasicrystal i-AlPdMn
The diffraction patterns of quasicrystals display both resolution-limited Bragg reflections and rotational symmetries incompatible with periodicity (as for instance the 5-fold symmetry). This particular type of long-range aperiodic order is referred to as quasiperiodicity. In a high-dimensional description of quasicrystals, the overall atomic arrangement in physical space (E//) can be viewed as a 3D section of a 6D periodic lattice decorated with 3D atomic domains defined in a complementary (or internal or perpendicular) space E.![]() When considering the symmetries that leave the i-phase free-energy invariant, we expect 6 hydrodynamic long-wavelength modes: 3 associated with rigid translations of the solid along E//, the usual acoustic phonons, and 3 associated to phase displacements along E
When considering the symmetries that leave the i-phase free-energy invariant, we expect 6 hydrodynamic long-wavelength modes: 3 associated with rigid translations of the solid along E//, the usual acoustic phonons, and 3 associated to phase displacements along E![]() , the so called phason degrees of freedom [1]. In quasicrystals, phasons correspond to internal atomic rearrangements, where atoms jump between sites with similar local environment. These jumps are correlated and the corresponding dynamical process is a diffusive one. A clear signature of the existence of long-wavelength phason fluctuations occurring in quasicrystals is the predicted and indeed observed specific anisotropy of the diffuse scattering near Bragg peaks [2]. However, the dynamics of phason fluctuations implies very slow relaxation times.
, the so called phason degrees of freedom [1]. In quasicrystals, phasons correspond to internal atomic rearrangements, where atoms jump between sites with similar local environment. These jumps are correlated and the corresponding dynamical process is a diffusive one. A clear signature of the existence of long-wavelength phason fluctuations occurring in quasicrystals is the predicted and indeed observed specific anisotropy of the diffuse scattering near Bragg peaks [2]. However, the dynamics of phason fluctuations implies very slow relaxation times.
X-ray Intensity Fluctuation Spectroscopy (XIFS) is a unique technique taking advantage of the coherence properties of the incident X-ray beam to study atomic length scale fluctuations of domains occurring on 10-3-103 s time scales [3]. With a coherent beam, the resulting intensity distribution exhibits a spiky structure originating from constructive and destructive interferences between scattering domains. Any time evolution of these scattering domains' distribution due to fluctuations in the sample results in a time evolution of the speckle intensity distribution.
Using XIFS on beamline ID20, we were able to make the first characterisation of the dynamics of long-wavelength phason fluctuations in the i-AlPdMn quasicrystalline phase. With a 10 µm pinhole just before the sample, the partial coherence ß of the set up was evaluated to 5% for the low angle 7/11 Bragg reflection. The scattering geometry of the entire set up allowed us to measure the diffuse intensity distribution for a range of phason wavevectors q centred around the (![]() ,-1,0) direction where
,-1,0) direction where ![]() = (1+
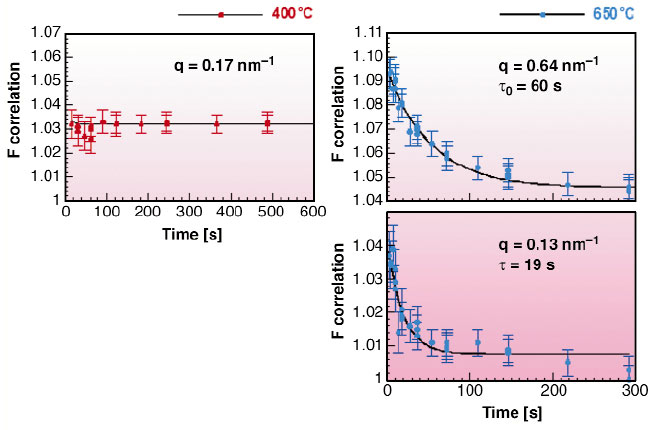
= (1+![]() 5)/2 is the golden mean. The diffuse scattering patterns were collected on a 2D CCD camera located at 1.85 m from the sample. A fast shutter on the incoming beam permitted a time acquisition of 1 to 5s and a time-dependence analysis of the intensity correlation from 2 to 1000 s. From room temperature up to 500°C, the intensity correlation function, defined as Fcorr.(q,t) = <I(q,t)(I(q,t+t')>t'/<I(q,t')>t'2 where < >t' is the average over a time t', was found to remain constant over the time of measurement. This behaviour is consistent with frozen-in phason fluctuations at low temperatures. Around 550°C, an activation of the diffusive process is perceptible with a very slow time evolution of Fcorr.(q,t). At 650°C, the intensity correlation function exhibits an exponential time dependence of the form Fcorr.(q,t)=1+ß.exp(-t/
5)/2 is the golden mean. The diffuse scattering patterns were collected on a 2D CCD camera located at 1.85 m from the sample. A fast shutter on the incoming beam permitted a time acquisition of 1 to 5s and a time-dependence analysis of the intensity correlation from 2 to 1000 s. From room temperature up to 500°C, the intensity correlation function, defined as Fcorr.(q,t) = <I(q,t)(I(q,t+t')>t'/<I(q,t')>t'2 where < >t' is the average over a time t', was found to remain constant over the time of measurement. This behaviour is consistent with frozen-in phason fluctuations at low temperatures. Around 550°C, an activation of the diffusive process is perceptible with a very slow time evolution of Fcorr.(q,t). At 650°C, the intensity correlation function exhibits an exponential time dependence of the form Fcorr.(q,t)=1+ß.exp(-t/![]() 0(q)) with a characteristic decay time
0(q)) with a characteristic decay time ![]() 0(q) decreasing as the phason wavevector q increases (see Figure 117). As expected for a diffusive process,
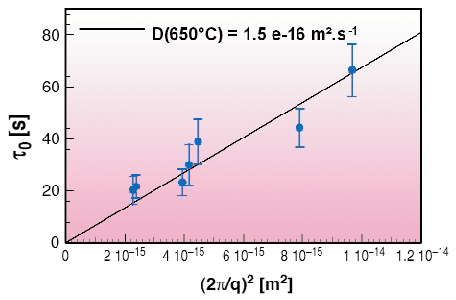
0(q) decreasing as the phason wavevector q increases (see Figure 117). As expected for a diffusive process, ![]() 0(q) obeys a q-2 law with a phason diffusion constant Dphason (650°C) = 1.5 10-16 m2.s-1 (see Figure 118). In principle, three phason modes contribute to the diffusive intensity. However, the mode with the slowest time constant dominates the measured signal and is the only one observed. Figure 118 can thus be regarded as a "dispersion" relation of a phason mode propagating along the (
0(q) obeys a q-2 law with a phason diffusion constant Dphason (650°C) = 1.5 10-16 m2.s-1 (see Figure 118). In principle, three phason modes contribute to the diffusive intensity. However, the mode with the slowest time constant dominates the measured signal and is the only one observed. Figure 118 can thus be regarded as a "dispersion" relation of a phason mode propagating along the (![]() ,-1, 0) direction with a polarisation along E
,-1, 0) direction with a polarisation along E![]() .
.
 |
|
Fig. 117: Correlation functions Fcorr..(q,t) for different temperatures and q phason wavevectors along the ( |
 |
|
Fig. 118: Evolution at 650°C of the characteristic decay |
References
[1] T.C. Lubensky et al., Phys. Rev. B 32(11), 7444 (1985).
[2] M. de Boissieu et al., Phys. Rev. Lett., 75, 89 (1995).
[3] M. Sutton, K. Laaziri, F. Livet, and F. Bley, Opt. Express 11, 2268-2277 (2003).
Authors
S. Francoual (a, b), F. Livet (a), M. de Boissieu (a), F. Yakhou (c), F. Bley (a), A. Létoublon (d), R. Caudron (e,f), J. Gastaldi (g), Phys. Rev. Lett. 91(22), 225501/1-225501/4 (2003).
(a) LTPCM, St Martin d'Heres (France)
(b) ILL
(c) ESRF
(d) DRFMC, SP2M, CEA-Grenoble (France)
(e) LEM, ONERA-CNRS, Chatillon (France)
(f) LLB, CEA-CNRS, Saclay (France)
(g) CRMC2, Marseille (France)



