- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2016
- Electronic structure, magnetism and dynamics
- Spiral spin-liquid and the emergence of a vortex-like state in MnSc2S4
Spiral spin-liquid and the emergence of a vortex-like state in MnSc2S4
Spiral spin-liquid is a short-range correlated state where spins fluctuate collectively as spirals in real space. Such a correlation is highly unusual: in conventional paramagnets, spins fluctuate in a completely random fashion. We present direct experimental evidence for the existence of the spiral spin-liquid state in A-site spinels, reveal the multi-step ordering of the spiral spin liquid and discover a vortex-like triple-q phase on application of a magnetic field.
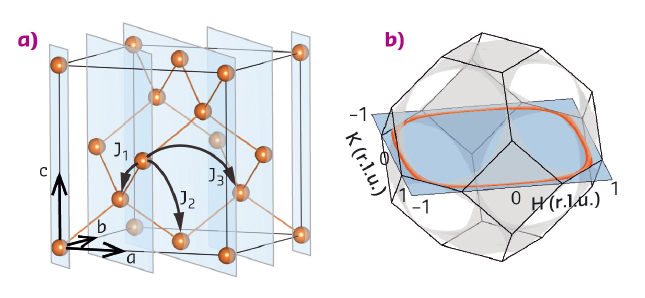
The A-site spinel MnSc2S4 is a promising candidate to realise the spiral spin-liquid state [1,2]. In MnSc2S4, Mn2+ (S = 5/2) ions occupy the A-sites and constitute a diamond lattice as is shown in Figure 27a. The bi-partite character of the diamond lattice allows the definition of the J1-J2 model, with the ferromagnetic J1 and the antiferromagnetic J2 couplings. In the weak frustration regime of J2/J1 < 0.125, the spin correlations are similar to that of conventional paramagnets. However, in the strong frustration regime of J2/J1 > 0.125, the propagation vector will form a continuous surface in the reciprocal space, shown in Figure 27b. Since each q-vector on this surface represents a spiral state under the mean-field theory, such a continuous surface is named the 'spiral surface'. Previous experiments using a powder sample of MnSc2S4 have revealed a long-range order transition at TN = 2.3 K and suggested the existence of the spiral surface at T > TN [3]. However, direct proof of the spiral surface was missing, which requires single crystal samples.
 |
|
Fig. 27: a) Mn2+ ions in MnSc2S4 constitute a diamond lattice. b) The predicted spiral surface (grey) in MnSc2S4 with the frustration ratio J2/J1 = 0.85. |
Recently we succeeded in growing single crystals of MnSc2S4 using the chemical transport technique. To check the quality, we performed single-crystal synchrotron diffraction experiments at beamline BM01 (Swiss-Norwegian CRG beamline). Altogether 2738 Bragg reflections were collected at room temperature, our refinement of the spinel structure did not detect any Mn-Sc anti-site disorder and confirmed the good quality of our single crystals.
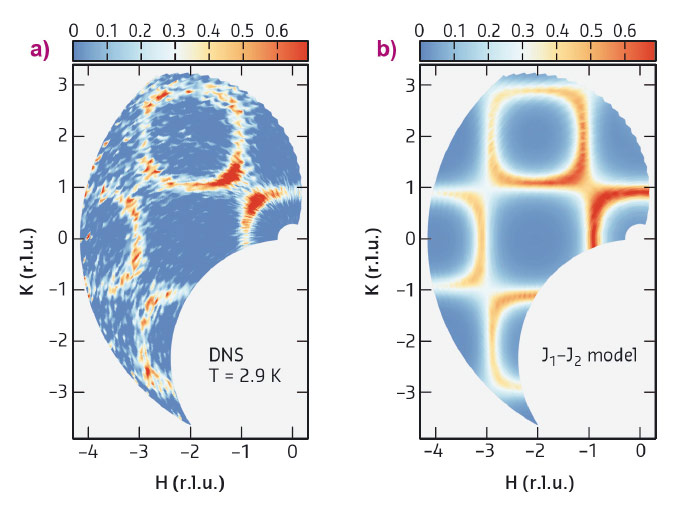
To study the short-range correlations in MnSc2S4, we performed polarised neutron diffuse scattering experiments on DNS at MLZ. Figure 28a presents the results measured at T = 2.9 K. A squared ring feature near the Brillouin zone boundary can be clearly resolved, which is consistent with the existence of the spiral surface. Considering that the spiral surface extends towards the zone boundary with increasing frustration ratio J2/J1, it is clear that the frustration should be strong in MnSc2S4.
 |
|
Fig. 28: a) Diffuse neutron scattering results measured on DNS at 2.9 K. The 50 K data has been subtracted as the background. b) Monte Carlo simulation results using the J1-J2 model with a frustration ratio of J2/J1 = 0.85. |
To fix the frustration ratio J2/J1 in MnSc2S4, we performed classical Monte Carlo simulations using the ALPS package [4]. As shown in Figure 28b, the simulation results with J2/J1 = 0.85 can reproduce the observed squared ring feature very well. Such a high ratio of J2/J1 puts MnSc2S4 deep in the spiral spin-liquid phase [1] and thus the observed ring feature is direct evidence of the spiral surface.
Besides the spiral spin-liquid state, we also investigated the long-range ordered state at T < TN performing single crystal neutron diffraction on TriCS at SINQ of PSI and spherical neutron polarimetry on TASP with MuPAD at SINQ and IN22 with CryoPAD at ILL. Our experiments revealed multi-step transitions: at 2.2 K, the system first enters a sinusoidally modulated collinear phase with q = [0.75 0.75 0]; at 1.64 K, it then enters a transitional incommensurate phase with q = [0.75±0.02 0.75±0.02 0]; and finally, at 1.46 K, the system enters a helical phase with q back to the [0.75 0.75 0] position. Such a multi-step transition is direct evidence of the importance of perturbations from the third-neighbour coupling J3 and the dipolar interactions [2].
Under a magnetic field along the [001] direction, a triple q phase with ∑i qi = 0 is observed through the analysis of the domain population. Although neutron diffraction is not sensitive to the phase factor, candidate structures all exhibit a winding feature for the spin components in the [111] plane. Therefore the observed triple-q structure is in fact a vortex lattice. We note that the q-combination rule of the triple-q phase is very similar to that of the skyrmion lattice [5].
Principal publication and authors
Spiral spin-liquid and the emergence of a vortex-like state in MnSc2S4, S. Gao (a,b), O. Zaharko (a), V. Tsurkan (c,d), Y. Su (e), J.S. White (a), G.S. Tucker (a,f), B. Roessli (a), F. Bourdarot (g), R. Sibille (a,h), D. Chernyshov (i), T. Fennell (a), A. Loidl (c) and C. Rüegg (a,b), Nature Physics (2016); doi: 10.1038/nphys3914.
(a) Laboratory for Neutron Scattering and Imaging, Paul Scherrer Institut, Villigen PSI (Switzerland)
(b) Department of Quantum Matter Physics, University of Geneva (Switzerland)
(c) Experimental Physics V, University of Augsburg (Germany)
(d) Institute of Applied Physics, Academy of Sciences of Moldova, Chisinau (Republic of Moldova)
(e) Jülich Center for Neutron Science JCNS-MLZ, Forshungszentrum Jülich GmbH, Outstation at MLZ, Garching (Germany)
(f) Laboratory for Quantum Magnetism, École Polytechnique Fédérale de Lausanne (Switzerland)
(g) CEA et Université Grenoble Alpes, INAC-MEM-MDN, Grenoble (France)
(h) Laboratory for Scientific Developments and Novel Materials, Paul Scherrer Institut, Villigen PSI (Switzerland)
(i) Swiss-Norwegian Beamlines at the ESRF, Grenoble (France)
References
[1] D. Bergman et al., Nat. Phys. 3, 487 (2007)
[2] S. B. Lee et al., Phys. Rev. B 78, 144417 (2008)
[3] A. Krimmel et al., Phys. Rev. B 73, 014413 (2006)
[4] B. Bauer et al., J. Stats. Mech. 2011, P05011 (2011)
[5] S. Mühlbauer et al., Sci. 323, 915 (2009).



