- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2010
- Structure of materials
- Graphene on Ir(111): A weakly bonded system
Graphene on Ir(111): A weakly bonded system
Since its successful isolation from graphite in 2004 (Nobel prize in physics 2010 for A. Geim and K. Novoselov), graphene has attracted a huge amount of interest for its extraordinary structural and electronic properties. Epitaxial growth is the most suitable method for the preparation of large-area, well-ordered films [1]. On specific surfaces [Pt(111), Ir(111)] the interaction between graphene and the substrate is so weak that graphene behaves as quasi-freestanding [2].
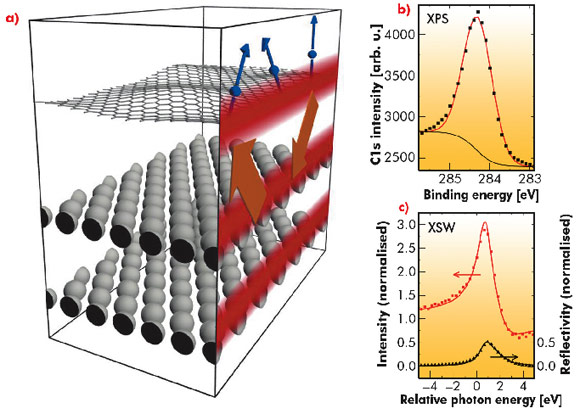
The exact structural parameters for model systems such as graphene on Ir(111) or graphene on Ru(0001) are debated in the literature. This is mainly due to the large unit cell of the structures caused by the lattice mismatch as well as to the difficulties inherent in standard density functional theory (DFT) calculations to include correctly the significant non-local van der Waals (vdW) interaction. To make a precise measurement of the height distribution of the carbon atoms in graphene on Ir(111), we performed an X-ray standing wave (XSW) analysis at beamline ID32. An X-ray standing wave is created in the interface region of a crystal using Bragg reflection (see Figure 36a). The maxima of the XSW, which are periodic with the Ir lattice planes, are shifted by half the lattice plane distance when scanning through the Bragg reflection by changing the beam energy. The carbon atoms in the maximum of the standing wave field display the maximum photoelectron yield. Therefore, scanning the XSW field through the different heights and monitoring the photoemission signal allows a determination of the average carbon atom height. For graphene/Ir(111), we derived a mean height of h = 3.38 ± 0.04 Å from the change in the area of the C1s peak in the photoelectron spectra (Figure 36b) at different photon energies (Figure 36c). This is similar to the interlayer distance in graphite (3.36 Å), which indicates that only weak bonding is present in this system.
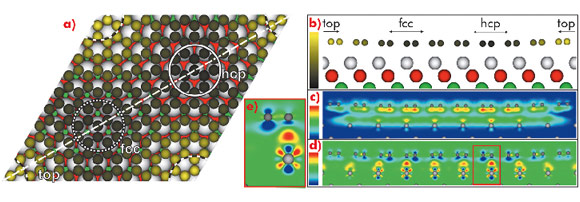
To complement these experimental results, we performed ab initio DFT calculations including the vdW interaction. The results are visualised in Figure 37, where a variation of the carbon heights within the unit cell is clearly visible, with the highest values found in regions where the centre of the C hexagon is located on top of an Ir atom (top region) and the lowest values found for C are at the hcp- and fcc-regions. The mean value is h = 3.41 Å, in good agreement with the experimental results.
The total binding energy found in our calculations is Eb = -50 meV/C, again similar to the corresponding value for graphite. Our advanced DFT approach makes it possible to divide the overall binding energy into nonlocal (i.e. vdW) contributions (-70 meV/C) and local (i.e. chemical) contributions (+20 meV/C, repulsion!). This shows that actually the vdW contribution (spatial distribution visualised in Figure 37c) dominates this system. Contrary to the impression given by the averaged values of the binding energies, the binding mechanism is not purely physisorption, although it is dominated by vdW. This becomes obvious when one studies the charge transfer caused by adsorption, visualised in Figure 37 (d and e). In the hcp- and fcc-regions, a small charge transfer from graphene to substrate takes place that leads to a charge accumulation at the graphene/Ir(111) interface. This indicates the formation of local bonding with a covalent character. Overall, the charge rearrangement leads to a shifting of the Dirac point to 0.2 eV above EFermi, which is consistent with experiment [2].
Principal publication and authors
C. Busse (a), P. Lazić (b), R. Djemour (a), J. Coraux (c), T. Gerber (a), N. Atodiresei (b), V. Caciuc (b), R. Brako (d), A.T. N'Diaye (a), S. Blügel (b), J. Zegenhagen (e) and T. Michely (a), submitted to PRL.
(a) II. Physikalisches Institut, Universität zu Köln (Germany)
(b) Institut für Festkörperforschung (IFF) and Institute for Advanced Simulation (IAS), Forschungszentrum Jülich and JARA, Jülich (Germany)
(c) Institut Néel, CNRS-UJF, Grenoble (France)
(d) Ru-der Bovskovi´c Institute, Zagreb (Croatia)
(e) ESRF
References
[1] J. Coraux, A.T. N'Diaye, C. Busse and T. Michely, Nano Lett. 8, 565 (2008).
[2] I. Pletikosi´c, M. Kralj, P. Pervan, R. Brako, J. Coraux, A.T. N'Diaye, C. Busse and T. Michely, Phys. Rev. Lett. 102, 056808 (2009).