- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2010
- Structure of materials
- A 3D look inside nanocrystals
A 3D look inside nanocrystals
Classically, images are produced by lenses, which allow magnification of the sample within the resolution limit given by the Rayleigh criterion. However, precise knowledge of the complex-valued scattered field would provide a detailed and correct image. Therefore, the application of lensless imaging techniques has earned much attention recently, especially in the X-ray domain. Indeed, X-rays – with a wavelength in the 0.1 nm range – are particularly useful for nanoscience, where a detailed knowledge of the internal structure on the nanoscale is of fundamental importance to understand the properties of nanostructures.
Fourier transform holography [1] is a lensless microscopy method based on measurements of the coherently diffracted intensity: its utility arises from its capacity to yield not only the amplitude of the scattered field but also to encode the phase in the diffraction pattern, thereby allowing solution of the “phase problem”. The phase information is contained in the interference of the coherently scattered waves from the sample and a reference. A single inverse Fourier transform of the intensity pattern allows direct reconstruction of the sample’s electron density distribution. Several X-ray holography examples have been reported in the literature [2], performed in the forward direction geometry (i.e. near the origin of reciprocal space) practically restricting the imaging to two dimensions.
A novel approach to determine the 3D crystal structure of nanoscale materials by the use of X-ray Fourier transform holography in Bragg geometry is demonstrated in this work. The possibility to investigate reciprocal space near one of the Bragg points offers several key advantages: (i) access to the 3D diffraction intensity pattern for a generalisation of the X-ray holography method to the 3D case and (ii) sensitivity to the displacement field in the crystal, with nanoscale resolution. These are of great interest as non-destructive measurements of the 3D displacement field are challenging at the nanoscale.
Similar to Fourier transform holography, this method’s Bragg approach makes use of the interference produced between the field scattered by the sample and a reference. However, in order to produce measurable interference in the vicinity of the sample Bragg peaks, a small crystalline reference, referred to as the reference crystal, with a lattice parameter close to that of the object crystal has to be located close to the object crystal. When these conditions are fulfilled, the sample’s electron density is obtained by a single inverse Fourier transform of the far-field intensity pattern. The displacement field information appears as a phase in the complex-valued electron density.
 |
|
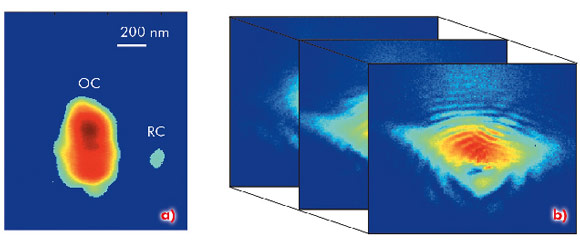
Fig. 26: a) The holographic sample: object (OC) and reference crystal (RC). b) 2D slices through the 3D coherent Bragg diffraction intensity distribution. |
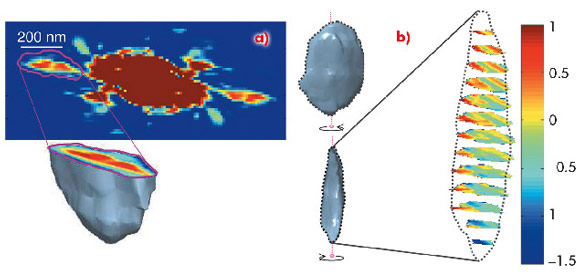
The sample used for this work consists of an object crystal and a small reference crystal (Figure 26a) produced by electron-beam lithography from a SiGe continuous layer (200 nm thick) on a Si (001) substrate. The experiment was carried out at beamline ID01. To increase the flux on the sample, a coherently illuminated Fresnel zone plate was used to produce a focussed coherent beam. The 3D coherently scattered intensity around the SiGe (004) Bragg peak was measured by a 2D Maxipix detector for different values of the rocking angle (Figure 26b). The observed low and high frequency fringes result from the interference of the waves scattered from the two crystals and are induced by their small and finite sizes. These slices are stacked in a 3D matrix for the inversion process: after a single inverse Fourier transform, retrieval of the 3D sample image is straightforward (Figure 27a). In addition to the shape, the internal view of the nanocrystal is obtained (Figure 27b), demonstrating the capability of the method to give access to the 3D description of the sample electron density and the displacement field.
 |
|
Fig. 27: a) The inverse Fourier transform of the 3D intensity distribution. b) Two views of the external shape and the internal phase distribution (colour scale in radians). |
The simplicity and robustness of the inversion using Bragg Fourier transform holography paves the way to in situ investigations of inhomogeneous strain fields in nanocrystals and thus will be beneficial to the understanding of current strain related problems in nanomaterials research.
Principal publication and authors
V. Chamard (a) J. Stangl (b), G. Carbone (c), A. Diaz (c), G. Chen (b), C. Alfonso (d), C. Mocuta (c) and T.H.Metzger (c), Phys. Rev. Lett. 104, 165501 (2010).
(a) Institut Fresnel, CNRS, Aix-Marseille University, Marseille (France)
(b) Institute of Semiconductor and Solid State Physics, Johannes Kepler Universität, Linz (Austria)
(c) ESRF
(d) IM2NP, CNRS, Aix-Marseille University, Marseille (France)
References
[1] D. Gabor, W.E. Kock, and G.W. Stroke, Science 173, 11 (1971).
[2] S. Eisebitt et al., Nature (London) 432, 885 (2004); L.-M. Stadler et al., Phys. Rev. Lett. 100, 245503 (2008).



