- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2009
- X-ray imaging
- Phase-contrast and holographic computed laminography
Phase-contrast and holographic computed laminography
Computed tomography is an established method for three-dimensional imaging at synchrotron sources. When applied to laterally extended specimens like plate-like objects, measurements are usually afflicted by artefacts due to the limited accessible angular range.
Recently, synchrotron radiation computed laminography was developed [1] to complement computed tomography for imaging of laterally extended specimens. Since the method enables us to zoom in to regions of interest of macroscopically large devices with microscopic resolution, it is optimised for acquisition and reconstruction of 3D data sets from rather flat specimens with lateral extensions much larger than the detector acceptance window. Like computed tomography, it takes advantage of the higher photon flux and high brilliance available at synchrotron sources resulting in a reduced data acquisition time and improved contrast due to the use of monochromatic radiation.
We have extended the applicability of laminography to high-resolution 3D imaging of weakly-absorbing specimens whose integrity needs to be preserved. This is especially important in the case of precious specimens, for materials which might suffer from sample extraction or when time-resolved measurements are required on a specimen under load and with engineering-relevant boundary conditions. The method uses the unique properties of partial coherence delivered through propagation-based phase contrast.
Computed laminography relaxes the geometrical requirements of computed tomography – which is characterised by tomographic rotation around an axis perpendicular to the beam path – to the more general case of using an inclined rotation axis. The flat specimen is mounted with its normal approximately parallel to the rotation axis.
Propagation-based phase contrast is included into computed laminography measurements via detecting the intensity patterns at varying propagation distances downstream of the laterally extended specimen. Similar to phase-contrast computed tomography, the principle of phase-contrast computed laminography can be divided into three steps: 1) radiographic data acquisition involving projection of the original 3D object function and wavefield propagation to finite detector distances; 2) retrieval of the corresponding two-dimensional phase and amplitude distribution maps; 3) reconstruction of the 3D laminographic image function for the specimen’s region of interest. Unlike in phase-contrast computed tomography, there exists a priori knowledge about the variation of the propagation distance along the projection of the rotation axis which can be included in the phase retrieval step 2 (see principal publication).
 |
|
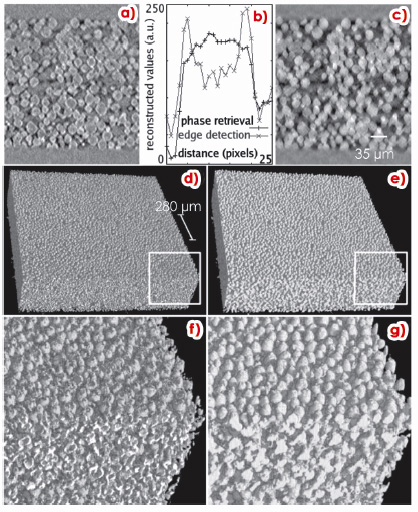
Fig. 145: Region-of-interest imaging of a diffusion layer sheet developed for fuel cells by phase-contrast laminography. For the edge-detection regime (a,d,f) a single specimen-detector distance of 0.03 m was used. For the holographic reconstruction (c,e,g) the distances 0.03, 0.045, 0.105 and 0.215 m were used. The images (a) and (c) are reconstructed cross-sectional slices along the direction of the rotation axis, the images (d) and (e) 3D renditions of the ROI imaged, with magnifications in (f) and (g), respectively. The plots (b) compare profiles in (a) and (c) along the line given in (c). Axis inclination 30°, X-ray energy 20.5 keV, voxel size 1.4 µm. |
Using the example of a diffusion layer developed for fuel cells, 3D data reconstructed by phase-contrast computed laminography are presented in Figure 145, both for the edge-detection regime (a,d,f) and for holographic phase retrieval (c,e,g). The diffusion layer consists of a sheet of interconnected spheres mainly made of carbon. When applying holographic phase retrieval [2] from four propagation distances, the reconstructed image (see c,e,g) is directly sensitive to the refractive index decrement distribution ![]() (x,y,z) so that contrast appears between the spheres’ volume material and the surrounding voids. This allows easy segmentation, generally not sensitive to noise [see the cross-sectional slice (c) and 3D rendition (e) with magnification in (g)]. When working with only one propagation distance in the edge-detection regime (see a,d,f), we are sensitive to the Laplacian of
(x,y,z) so that contrast appears between the spheres’ volume material and the surrounding voids. This allows easy segmentation, generally not sensitive to noise [see the cross-sectional slice (c) and 3D rendition (e) with magnification in (g)]. When working with only one propagation distance in the edge-detection regime (see a,d,f), we are sensitive to the Laplacian of ![]() (x,y,z). As a result, the surfaces of the microparticles become emphasised in the image. In many cases, this already gives sufficient information about the specimen’s structure at the region of interest investigated. For a more quantitative comparison, cuts through a single sphere are compared by the profiles in (b).
(x,y,z). As a result, the surfaces of the microparticles become emphasised in the image. In many cases, this already gives sufficient information about the specimen’s structure at the region of interest investigated. For a more quantitative comparison, cuts through a single sphere are compared by the profiles in (b).
The results demonstrate the feasibility of laminographic phase-contrast techniques. It is noteworthy that, contrary to computed tomography, the images are acquired without any specimen preparation (i.e. sample extraction), just by zooming into the region of interest of a macroscopically large specimen.
In summary, phase-contrast laminography complements phase-contrast computed tomography for non-destructive 3D imaging of weakly contrasted structures. The Karlsruhe Institute for Technology has installed a dedicated instrument for computed laminography at beamline ID19. By completely avoiding a transilluminated specimen holder it is especially adapted to phase-contrast measurements. It allows one to zoom into arbitrary regions of interest and to scan macroscopically large specimen areas of up to 150x150 mm with spatial resolutions presently down to the micrometre scale. Avoiding the need for destructive sample extraction, the method and its instrumental realisation will provide new insight into microstructures and their evolution in application fields where layers, sheets or panels of light (e.g. organic) materials are used; for example in biological specimens, filter materials, paints and paintings or composite materials.
References
[1] L. Helfen, T. Baumbach, P. Mikulík, D. Kiel, P. Pernot, P. Cloetens and J. Baruchel. Appl. Phys. Lett. 86, 071915 (2005).
[2] P. Cloetens, W. Ludwig, J. Baruchel, D. van Dyck, J. van Landuyt, J.P. Guigay and M. Schlenker, Appl. Phys. Lett. 75, 2912 (1999).
Principal publication and authors
L. Helfen (a), T. Baumbach (a), P. Cloetens (b) and J. Baruchel (b), Appl. Phys. Lett. 94, 104103 (2009).
(a) Institute for Synchrotron Radiation (ISS/ANKA), Karlsruhe Institute of Technology (Germany)
(b) ESRF



