- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2005
- Soft Condensed Matter
- X-ray Intensity Fluctuation Spectroscopy (XIFS) Studies of Ordering Kinetics in a Cu-Pd Alloy
X-ray Intensity Fluctuation Spectroscopy (XIFS) Studies of Ordering Kinetics in a Cu-Pd Alloy
A number of studies have used XIFS (also known as X-ray Photon Correlation Spectroscopy, XPCS) to examine fluctuation dynamics particularly in soft condensed matter, but few have attempted to use it to probe the kinetics of phase transitions. Here we report a XIFS study of the ordering kinetics in the classic long-period superlattice (LPS) alloy Cu-Pd using the ID10A “Troïka” beamline. In such LPS alloys there can be an equilibrium periodic modulation of the atomic order in one or two dimensions, giving a complex alloy structure. In order to better understand the complicated ordering process, this study examines the two-time pair-correlation function C(q,t1,t2) during the ordering process on length scales of 101-103 nm and time scales of 102-104 sec. This corresponds to the regime of late-stage domain coarsening in the alloy. This two-time correlation function contains information beyond that available from the structure factor S(q,t) obtained from traditional time-resolved X-ray scattering experiments. In contrast to the situation for equilibrium speckle measurements, the two-time correlation function is necessary due to temporal evolution of the nonequilibrium system.
To investigate the behaviour of C(q,t1,t2), the evolution of both superlattice and satellite peaks, which are sensitive to local order and modulated order respectively, were examined. Figure 60 shows a typical speckle pattern obtained from the (100) superlattice peak during the ordering process. Theory and simulations [1] suggest that, with increasing time, the speckles themselves become longer lived. Indeed comparison of the different experimental speckle patterns taken as the domain coarsening progressed shows that individual speckles develop with lifetimes comparable to the duration of the experiment. Interestingly, the peak centres move a small amount during the coarsening process, but examination of the speckle patterns shows that the speckles themselves do not follow this motion. This unexpected phenomenon may be due to the elimination of lattice distortions distributed inhomogeneously in the sample at domain boundaries2 during the ordering process.
 |
|
Fig. 60: Speckles in the superlattice peak after 35991 s of ordering. Dark regions around the image edge are due to masking of the scattered X-rays. |
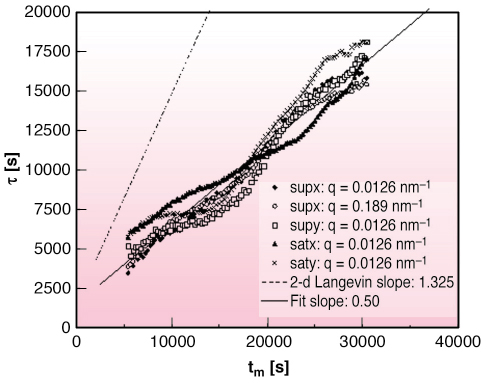
In the coarsening regime, the two-time pair-correlation function, C(q,![]() t,tm) with
t,tm) with ![]() t = |t2-t1| and tm = (t1+t2) / 2 , should obey scaling laws [1]. In particular, they predict that close to the central part of the peak the characteristic decay time of the two-time correlation function is proportional to the mean coarsening time tm. Figure 61 shows the experimental results. As predicted by theory, the experimentally determined correlation decay time increases linearly with tm.
t = |t2-t1| and tm = (t1+t2) / 2 , should obey scaling laws [1]. In particular, they predict that close to the central part of the peak the characteristic decay time of the two-time correlation function is proportional to the mean coarsening time tm. Figure 61 shows the experimental results. As predicted by theory, the experimentally determined correlation decay time increases linearly with tm.
 |
|
Fig. 61: Half-width decay time t of the normalised two-time correlation functions Cnorm(q,tm, |
One notable difference between predictions of theory/simulation and these experimental results, however, is the significantly slower rate of growth of the correlation decay time ![]() observed here. The
observed here. The ![]() /tm slope is a dimensionless quantity. Langevin calculations and simulations give a
/tm slope is a dimensionless quantity. Langevin calculations and simulations give a ![]() /tm slope of 1.325 in two dimensions. In three dimensions, the Langevin model would give a slightly higher ratio. In contrast, the observed slopes in both the superlattice and the satellite peaks are approximately 0.50. In the coarsening regime, the elapsed time is proportional to the square of average domain size and the correlation time measures the rate of structural rearrangements in the crystal. This slope therefore might be viewed as measuring how efficiently structural rearrangements lead to average domain growth with increasing coarsening. The low measured slope suggests that the growing average domain size leads to more structural rearrangement than is the case in the Langevin model. However, it is difficult to understand why this would be the case, and this remains an issue for future exploration.
/tm slope of 1.325 in two dimensions. In three dimensions, the Langevin model would give a slightly higher ratio. In contrast, the observed slopes in both the superlattice and the satellite peaks are approximately 0.50. In the coarsening regime, the elapsed time is proportional to the square of average domain size and the correlation time measures the rate of structural rearrangements in the crystal. This slope therefore might be viewed as measuring how efficiently structural rearrangements lead to average domain growth with increasing coarsening. The low measured slope suggests that the growing average domain size leads to more structural rearrangement than is the case in the Langevin model. However, it is difficult to understand why this would be the case, and this remains an issue for future exploration.
References
[1] G. Brown, P.A. Rikvold, M. Sutton and M. Grant, Phys. Rev. E 56, 6601 (1997).
[2] A. Fluerasu, M. Sutton and E.M. Dufresne, Phys. Rev. Lett. 94, 055501 (2005).
Principal Publication and Authors
K. Ludwig (a,b), F. Livet (a), F. Bley (a), J.-P. Simon (a), R. Caudron (c,d), D. Le Bolloc’h (e), A. Moussaid (f), Phys. Rev. B 72, 144201 (2005).
(a) LTPCM-ENSEEG-INPG, Saint Martin d’Hères (France)
(b) Permanent address: Boston University (USA)
(c) ONERA-LEM, Chatillon (France).
(d) Laboratoire Léon Brillouin, Saclay, Gif-sur-Yvette (France)
(e) Laboratoire de Physique des Solides, Orsay (France)
(f) ESRF



