- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2005
- Materials Science
- Excess Free Volume deltaVf in Metallic Glasses Measured by X-ray Diffraction
Excess Free Volume deltaVf in Metallic Glasses Measured by X-ray Diffraction
Excess Free Volume deltaVf in Metallic Glasses Measured by X-ray Diffraction
In 1960, Simmons and Balluffi [1] measured the concentration of lattice vacancies Cv(T) in crystals. They used the lattice parameter change ![]() a (T)/ao measured by X-ray diffraction to remove the part of the length-change due to the thermal expansion of the lattice measured by dilatometry
a (T)/ao measured by X-ray diffraction to remove the part of the length-change due to the thermal expansion of the lattice measured by dilatometry ![]() L (T)/Lo. What remains of
L (T)/Lo. What remains of ![]() L (T)/Lo then yields the increase in vacant lattice sites.
L (T)/Lo then yields the increase in vacant lattice sites.
Their experiments which contributed to the quantitative understanding of point defects in solid-state physics were based on:
|
|
where ![]() a (T) /ao =
a (T) /ao = ![]() th (T) * (T-To) / ao , Lo and ao are the crystal length and lattice parameter at a reference temperature To, and
th (T) * (T-To) / ao , Lo and ao are the crystal length and lattice parameter at a reference temperature To, and ![]() th (T) the linear coefficient of thermal expansion.
th (T) the linear coefficient of thermal expansion.
The quenched-in free-volume, ![]() Vf, controls atomic mobility in metallic glasses like vacancies do in crystals. Hence, for the present experiment, our aim was to discover whether quenched-in free-volume takes the form of atomic-sized holes in the glassy state as in crystals. To discover this, a combination of dilatation and X-ray diffraction measurements would be needed to determine
Vf, controls atomic mobility in metallic glasses like vacancies do in crystals. Hence, for the present experiment, our aim was to discover whether quenched-in free-volume takes the form of atomic-sized holes in the glassy state as in crystals. To discover this, a combination of dilatation and X-ray diffraction measurements would be needed to determine ![]() Vf in the same way as for vacancies Cv(T) in crystals. On the other hand, computer simulation predicts [2] atomic size holes or vacancies in the glass are unstable and the quenched-in free volume in liquids and glasses is randomly distributed. If this were the case, then eq.(1) of Simmoms and Balluffi would not apply,
Vf in the same way as for vacancies Cv(T) in crystals. On the other hand, computer simulation predicts [2] atomic size holes or vacancies in the glass are unstable and the quenched-in free volume in liquids and glasses is randomly distributed. If this were the case, then eq.(1) of Simmoms and Balluffi would not apply, ![]() V (T) /Vo would be equal to 3
V (T) /Vo would be equal to 3![]() L(T)/Lo and the mean atomic volume and the sample dimensions would evolve together with temperature.
L(T)/Lo and the mean atomic volume and the sample dimensions would evolve together with temperature.
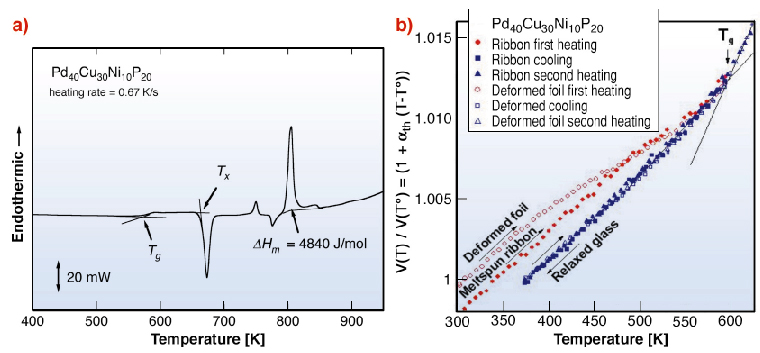
Using diffraction in transmission, we determined the evolution of the “average” interatomic distance and the excess free volume ![]() Vf from the difference between the interatomic distance versus temperature curves (dilatation) during initial heating to the supercooled liquid state above the glass transition Tg (see Figure 42a) of the quenched glass (containing
Vf from the difference between the interatomic distance versus temperature curves (dilatation) during initial heating to the supercooled liquid state above the glass transition Tg (see Figure 42a) of the quenched glass (containing ![]() Vf) versus the second heating of the then relaxed glass having already been heated to Tg (with
Vf) versus the second heating of the then relaxed glass having already been heated to Tg (with ![]() Vf annealed out).
Vf annealed out). ![]() Vf were found to be about 2000 ppm in quenched metallic glasses. Deformation-induced
Vf were found to be about 2000 ppm in quenched metallic glasses. Deformation-induced ![]() Vf was also measured (about 5000 ppm). Dilatation curves (see Figure 42b) were found to be identical to those obtained by dialatometry to within experimental error (see ref. [3]). This indicates that, contrary to the Simmons and Balluffi formulation eq.(1) for crystals, the situation is different for metallic glasses,
Vf was also measured (about 5000 ppm). Dilatation curves (see Figure 42b) were found to be identical to those obtained by dialatometry to within experimental error (see ref. [3]). This indicates that, contrary to the Simmons and Balluffi formulation eq.(1) for crystals, the situation is different for metallic glasses, ![]() L(T) /Lo =
L(T) /Lo = ![]() a(T) /ao, and atomic-size holes are unstable with
a(T) /ao, and atomic-size holes are unstable with ![]() Vf distributed randomly, as predicted by simulation [2]. The measured thermal expansion coefficients
Vf distributed randomly, as predicted by simulation [2]. The measured thermal expansion coefficients ![]() th were the same as for dilatometry. The glass transition Tg appeared as a break in the value of
th were the same as for dilatometry. The glass transition Tg appeared as a break in the value of ![]() th at Tg.
th at Tg.
 |
|
Fig. 42: (a) Calorimetric data of a Pd-based glass [3]; (b) Reduced volume per atom measured by XRD showing relaxation in the as-quenched state and after heavy deformation of the glass towards the same relaxed glassy state at Tg. |
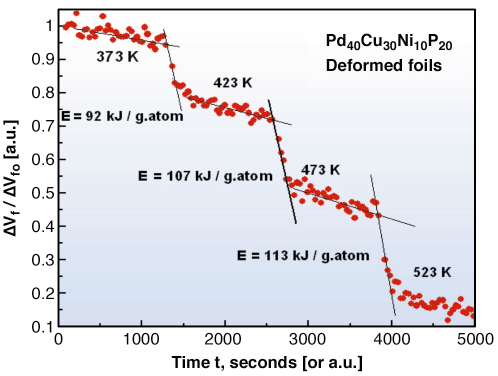
Metallic glasses are of the “fragile” type corresponding to an activation energy E for relaxation that increases with T (a non-Arrhenius behaviour) as expected, for example, for a Vogel–Fultcher–Tamman viscosity relation. If during isothermal relaxation, the temperature is abruptly changed at time t* from T1 to T2, the activation energy E can be obtained from the slope change according to [4]:
|
|
Figure 43 shows the result of such experiments. E increases from 92 kJ/g.at near 400 K to 114 kJ/g at near 500 K. Our new understanding of relaxation kinetics has allowed us to perform in situ fabrication of bulk metallic glasses (BMG-based) nanocomposites with enhanced ductility for structural applications.
 |
|
Fig. 43: Isothermal relaxation kinetics of excess free volume |
Acknowledgements
This work was performed in the framework of the EU Network contract (MRTN-CT-2003-504692 <Ductile BMG Composites>).
References
[1] R. Simmons and R. Balluffi R. Phys. Rev. 117-121 (1960).
[2] C.H. Bennett, P. Chaudhari, V. Moruzzi and P. Steinhardt Philo. Mag. A. 40, 485-489 (1979) .
[3] H.S. Chen, J. Appl. Phys. 49, 3289-3291 (1978).
[4] A.C. Damask and G.J. Dienes “Point Defects in Metals” Gordon and Breach, pp. 146-149 (1963).
Principal Publication and Authors
A.R. Yavari (a), A. Le Moulec (a), A. Inoue (b), N. Nishiyama (b), N. Lupu (a,b,c), E. Matsubara (b), W.J. Botta (a), G. Vaughan (c), M. di Michiel (c) , Å. Kvick (c), Acta Materialia, 53, 1611-1619 (2005).
(a) Euronano, LTPCM-CNRS, Institut National Polytechnique de Grenoble (France)
(b) Institute for Materials Research, Tohoku University, Sendai (Japan)
(c) ESRF



