- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2005
- High Resolution and Resonance Scattering
- Phonon Density of States Probed by Inelastic X-ray Scattering
Phonon Density of States Probed by Inelastic X-ray Scattering
The shape of the frequency distribution function g(![]() ) of the normal modes of vibration of a crystal determines an important part of its properties, since it contains many relevant elastic and thermodynamic information. From the overall spectrum, temperature dependencies of the lattice contribution to the specific heat and the internal energy, the vibrational entropy, the mean force constant and the Debye temperature are obtained, whereas from the low frequency part the Debye velocity can be derived, giving access to aggregate elastic properties. Experimentally, g(
) of the normal modes of vibration of a crystal determines an important part of its properties, since it contains many relevant elastic and thermodynamic information. From the overall spectrum, temperature dependencies of the lattice contribution to the specific heat and the internal energy, the vibrational entropy, the mean force constant and the Debye temperature are obtained, whereas from the low frequency part the Debye velocity can be derived, giving access to aggregate elastic properties. Experimentally, g(![]() ), or the vibrational density of states (VDOS), is commonly determined by inelastic neutron scattering (INS) or by nuclear inelastic scattering. Here, we show that inelastic X-ray scattering (IXS) offers an alternative experimental method.
), or the vibrational density of states (VDOS), is commonly determined by inelastic neutron scattering (INS) or by nuclear inelastic scattering. Here, we show that inelastic X-ray scattering (IXS) offers an alternative experimental method.
In analogy to coherent INS, inelastic scattering spectra of polycrystalline samples have to be recorded over a large range of momentum transfers (Q), but due to the Q-dependence of the atomic form factor, this sampling range needs to be optimised. We have developed semi-quantitative criteria, which are independent of any specific lattice dynamics model, and result only from simple symmetry considerations. The advantage of their use is that no a priori knowledge of the lattice properties is needed. The validity of our approach was checked by comparison of results for diamond with ab initio lattice dynamics calculations [1] and thermodynamic measurements.
The experiment was performed on ID28, utilising the silicon (9 9 9) setup, providing a total energy resolution of 3.0 meV. The momentum resolution was set to 0.7 nm-1 both in horizontal and vertical directions. As the spectrometer arm is equipped with five analysers, the spectra were recorded for two angular settings of the spectrometer arm, thus covering a Q-range from 60 to 75 nm-1 (approximately) and yielding ten IXS spectra. The total acquisition time per point was ~ 235 s with a maximum inelastic count rate of ~ 2.5 s-1. The sample was polycrystalline diamond with an average grain size of 3-5 µm, and the resulting effective scattering volume amounted to 0.08 mm3. For the data treatment we followed the same approach as for nuclear inelastic scattering, where the multiphonon term is eliminated simultaneously with the deconvolution of the data with the instrumental function [2].
 |
|
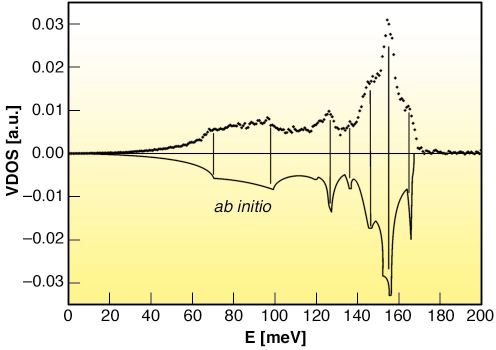
Fig. 16: Reconstructed vibrational density of states of diamond vs. calculated ab initio results [1]. |
Figure 16 shows the VDOS obtained, together with the result of an ab initio calculation [1]. The agreement is quite remarkable: the position of special points is nearly identical, and the high-energy peak, due to the overbending of the optical phonon branch, is clearly visible.
The excellent quality of our experimental VDOS allowed the determination of several macroscopic parameters such as the specific heat at constant volume, the low- and high-temperature limit of the Debye temperature ![]() D, and the Debye velocity VD. Table 1 shows a selection of our derived macroscopic parameters, compared to other experimental results.
D, and the Debye velocity VD. Table 1 shows a selection of our derived macroscopic parameters, compared to other experimental results.
 |
|
Table 1: Selected macroscopic parameters for diamond. |
The VDOS data were complemented by IXS measurements in the low-Q region which provide the orientationally averaged longitudinal acoustic dispersion. The resulting sound velocity VL = 18.24 km/s, combined with the Debye velocity VD, allows the extraction of the effective shear velocity VS = 12.43 km/s. These values give an appropriate description of the macroscopic aggregate elasticity of diamond.
Further experiments were performed on MgO, BN (zincblende and wurtzite polymorphs) and various ice polymorphs. The general applicability of the method for the study of elementary solids is easily estimated, showing that the VDOS can be determined with an appropriate accuracy for essentially all elemental solids. One of the potential applications of this novel technique is the VDOS determination of samples submitted to very high pressures. In this case the signal level for elements heavier than, say, scandium should be sufficiently high to allow measurements on tiny amounts of samples as in a diamond anvil cell.
It is worth noting that with respect to INS, the amount of material needed is 3-5 orders less, and anomalous absorption (like for B, Cd, Gd…) or anomalously high cross-sections (H) are not present. Since the scattering strengths for neutrons and X-rays are essentially different, it opens the possibility to extract directly the partial densities of states in at least binary systems from combined measurements.
References
[1] P. Pavone et al., Phys. Rev. B, 48, 3156-3163 (1993).
[2] V.G. Kohn and A.I. Chumakov, Hyperfine Interactions 125, 205-221 (2000).
[3] E.S. Zouboulis, M. Grimsditch, A.K. Ramdas, S. Rodriguez, Phys.Rev. B, 57, 2889-2896 (1988).
[4] Specific heat: non-metallic solids. Eds. Y.S. Touloukian, E.H. Buyco, IFI/Plenum New York – Washington 1970.
Principal Publication and Authors
A. Bosak, M. Krisch, in press, Phys. Rev. B; in press, Radiation Physics and Chemistry.
ESRF



