- Home
- News
- Spotlight on Science
- Atomic vibrations...
Atomic vibrations in nanocrystalline materials: does size really matter?
20-08-2008
The atomic dynamics in nanocrystalline solids are remarkably different from their bulk counterparts. The anomalous features are usually attributed to small nanograins with enhanced surface-to-volume ratio. An experiment performed at the ESRF unexpectedly shows that the atomic vibrations in nanograins are identical to those in the bulk even for extremely small grain sizes. The anomalous dynamics of nanocrystalline materials arises in fact from the atomic vibrations in the interfaces.
Nanocrystalline materials have already played an important role in mankind’s history, their use ranging from ancient Damascan swords [1] to modern lithium batteries [2]. Today the physics of nanocrystalline solids continues to attract growing interest due to their extraordinary properties such as enhanced hardness, enlarged plasticity, and superior magnetic properties. Accordingly, there is a continuously increasing number of industrial applications of these materials. Since the elastic properties are tightly related to the lattice dynamics, clear understanding of the atomic vibrations in nanocrystalline materials is important. A key characteristic of atomic dynamics is the density of phonon states (DOS), which gives a frequency spectrum of atomic vibrations and provides a complete description of the elastic and thermodynamic properties. The experimentally-determined DOS of nanocrystalline systems reveals striking anomalies such as broadening of the phonon peaks and enhancement of the phonon states at low and high energies [3]. These anomalies are generally believed to result from atoms at the nanograin surface, which can amount to ~65% of the volume for a grain of 2 nm in size. In addition, the energy dependence of the low-energy phonon states has been a source of long-standing debate. The experimental results are contradictory reporting a linear dependence [4], a power law with n=1.3 [5], and Debye behaviour [3]. Theoretical calculations have also indicated that non-Debye dynamics could originate from the atoms located at the surfaces [6], at the grain boundaries [7] or in the porous areas [8] of the nanocrystalline materials.
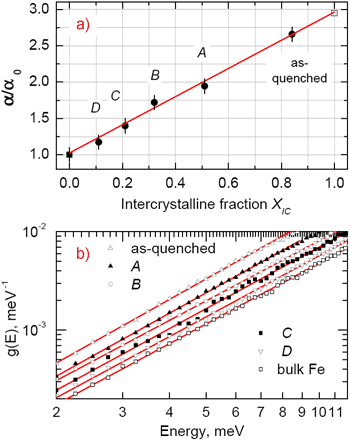
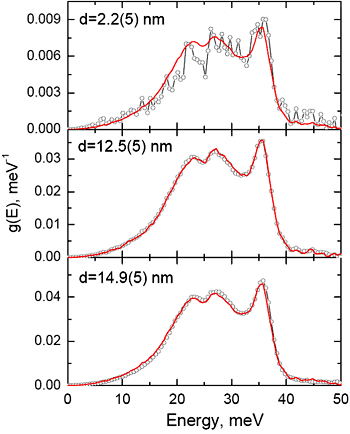
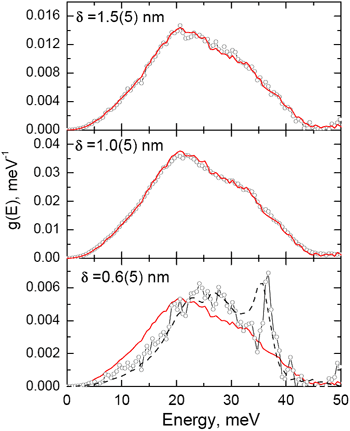
To further research the origin of these anomalies, scientists investigated the atomic dynamics of a nanocrystalline Fe90Zr7B3 alloy at ESRF beamline ID18. The nanocrystalline alloy had been prepared by crystallisation of an amorphous precursor. The high sensitivity of Mössbauer spectroscopy to the local environment of the resonant nuclei was employed to identify the amount of atoms located in the nanograins and in the interfaces for various crystallisation states. This allowed a systematic study of the DOS of the nanograins for a wide range of grain sizes (Figure 1) and the DOS of the interfaces for a wide range of thicknesses (Figure 2). Surprisingly, the results show that the density of states of the nanograins does not vary with the grain size and closely resembles that of bulk material down to the grains size of 2 nm. The observed anomalous features belong entirely to the interface atoms (Figure 3a). In addition, for all samples the low-energy part of their DOS follows the Debye approximation (Figure 3b), which excludes the presence of low-dimensional effects. Thus the results give unambiguous evidence that the anomalous dynamics and thermodynamics of nanocrystalline solids originate from the interfaces characterised with a certain degree of structural disorder, while the atoms building the nanograins vibrate in a bulk-like manner.
 |
|
Figure 1. Density of phonon states of the nanograins as a function of their size d. |
 |
|
Figure 2. Density of phonon states of the interfaces as a function of their thickness δ. |
An important practical implication of these findings is that tailoring of thermodynamic and elastic properties of nanocrystalline materials requires precise control of the interface fraction rather than of the nanograins size.
References
[1] T.H. Maugh, Science 215, 153 (1982).
[2] Y.-S. Hu et al., Nature Materials 5, 713 (2006).
[3] B. Fultz et al., Phys. Rev. Lett. 79, 937 (1997).
[4] U. Stuhr et al., Phys. Rev. Lett. 81, 1449 (1998).
[5] B. Roldan Cuenya et al., Phys. Rev. B 76, 195422 (2007).
[6] A. Kara and T.S. Rahman, Phys. Rev. Lett. 81, 1453 (1998).
[7] P. M. Derlet et al., Phys. Rev. Lett. 87, 205501 (2001).
[8] C. Hudon et al., Phys. Rev. B 76, 045409 (2007).
Principal publication and authors
S. Stankov (a), Y.Z. Yue (b,c), M. Miglierini (d), B. Sepiol (e), I. Sergueev (a), A.I. Chumakov (a), L. Hue (b,c), P. Svec (f), R. Rüffer (a), Vibrational properties of nanograins and interfaces in nanocrystalline materials, Phys. Rev. Lett. 100, 235503 (2008).
(a) ESRF
(b) Aalborg University, Aalborg (Denmark)
(c) Shandong University, Jinan (China)
(d) Slovak University of Technology, Bratislava (Slovakia)
(e) University of Vienna, Vienna (Austria)
(f) Slovak Academy of Sciences, Bratislava (Slovakia)