- Home
- News
- Spotlight on Science
- Phonon anomalies...
Phonon anomalies and the Verwey transition in magnetite
15-05-2013
The Verwey transition in magnetite is one of the longest unsolved problems of solid state physics, where the otherwise excellent theories fail to capture the collective nature of the first-order phase transition. A recent inelastic X-ray scattering (IXS) study revealed an anomalous broadening of specific phonon modes in a broad temperature range down to the Verwey transition at 124 K. Accompanying ab initio lattice dynamics calculations suggest the origin of this broadening to be strong phonon anharmonicity induced by electron-phonon coupling, thus indicating that the Verwey transition is a cooperative phenomenon which involves a wide spectrum of phonons coupled to the electron charge fluctuations.
Discovered in ancient Greece, magnetite (Fe3O4) played a crucial role in the history of Earth. It is well known for its extensive use in traditional recording media, but also for its role in the emerging field of spin electronic applications. Apart from its magnetic properties, which found numerous technological applications during the last century, magnetite exhibits extraordinary behaviour connected with the Verwey transition [1]. The most prominent feature observed upon lowering the temperature is the discontinuous reduction of the electric conductivity by two orders of magnitude at TV = 124 K, but spectacular anomalies occur in practically all physical properties. Extensive experimental and theoretical studies of magnetite during the last decades revealed very complex interrelations between the electronic and structural degrees of freedom, which both participate in the Verwey phase transition [2, 3]. Despite this progress, the transition is not yet fully understood and remains a very intriguing phenomenon in condensed matter physics. The low-temperature crystal structure was only solved very recently, and revealed a complex charge-order pattern, with a wide distribution of valencies at the octahedral sites, and an orbitally-ordered pattern distributed over three Fe sites [4].
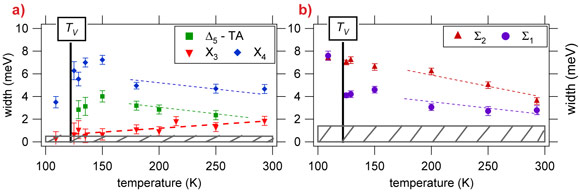
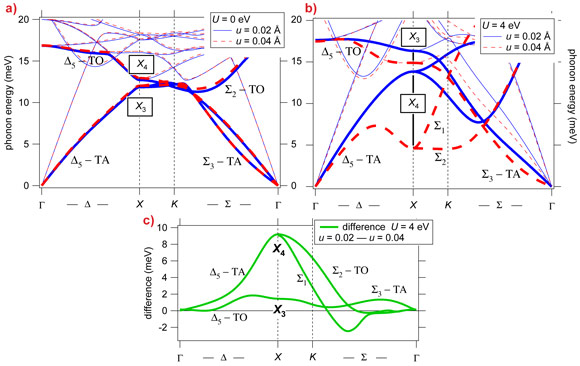
A recent lattice dynamics study of magnetite above TV carried out at beamline ID28 addresses the question whether or not the electron-phonon coupling in the presence of charge-order fluctuations is the principal cause of the Verwey transition. The experimental work reveals an increasing anomalous broadening of the lowest transverse acoustic (TA) phonon modes along the [001] (Δ) and transverse optic (TO) modes along the [110] (Σ) directions as temperature decreases towards TV (see Figure 1). Density functional theory (DFT) calculations show that the anharmonic phonon behaviour discovered here is (i) a direct consequence of the electron-phonon coupling, and (ii) occurs only in the presence of strong electronic correlations which is a novel aspect of the Verwey transition (see Figure 2).
In standard theories, large phonon widths indicate either an anharmonic behaviour or strong electron-phonon coupling. The present ab initio study demonstrates that these two effects are intimately connected in magnetite and both result from local electron interactions. These interactions induce polarisation of the minority-spin partly occupied t2g orbitals. In such a correlated state, the coupling between electrons and lattice enhances and stabilises the charge-orbital order, effectively reducing the total energy. This in turn modifies the interatomic interactions and generates the anharmonic potential. This mechanism leads to the Verwey transition with the static structural distortion and frozen charge-orbital order below TV. In contrast, above TV the charge-orbital degrees of freedom are dynamic and couple strongly to phonons reducing their lifetimes.
Principal publication and authors
Anharmonicity due to electron-phonon coupling in magnetite, M. Hoesch (a), P. Piekarz (b), A. Bosak (c), M. Le Tacon (d), M. Krisch (c), A. Kozłowski (e), A.M. Oleś (d,f), and K. Parlinski (b), Phys. Rev. Lett. 110, 207204 (2013).
(a) Diamond Light Source, Harwell Campus, Didcot (U.K.)
(b) Institute of Nuclear Physics, Polish Academy of Sciences, Kraków (Poland)
(c) ESRF
(d) Max-Planck-Institut für Festkörperforschung, Stuttgart (Germany)
(e) Faculty of Physics and Applied Computer Science, AGH University of Science and Technology, Kraków (Poland)
(f) Marian Smoluchowski Institute of Physics, Jagellonian University, Kraków (Poland)
References
[1] E.J.W. Verwey, Nature (London) 144, 327 (1939).
[2] M. Imada, A. Fujimori, and Y. Tokura, Rev. Mod. Phys. 70, 1039 (1998).
[3] F. Walz, J. Phys. Condens. Matter 14, R285 (2002).
[4] M.R. Senn, J.P. Wright, and J. P. Attfield, Nature (London) 481, 173 (2012).
Top image: Magnetite crystals (Credit: Rob Lavinsky, iRocks.com – CC-BY-SA-3.0).