- Home
- News
- Spotlight on Science
- Atomic dynamics...
Atomic dynamics and physical ageing in metallic glasses
13-11-2012
Glasses are often considered as archetypes for systems far from thermodynamical equilibrium. Understanding their physical ageing is essential for technological applications as well as for fundamental research. For the first time, researchers have investigated the ageing of metallic glasses at the atomic length scale. They found strong similarities between the behaviour of metallic glasses and the behaviour of many soft materials, suggesting the existence of a universal mechanism driving the ageing of out-of-equilibrium systems.
Many disordered materials, like glasses, polymers, gels and other soft materials undergo structural arrest and physical ageing [1]. Following different experimental routes, these materials can be driven in an out-of-equilibrium configuration, where the dynamics slow down enormously, and depends on the sample age or waiting time tw. A full understanding of ageing requires a detailed description of the particle-level dynamics, and of the structural relaxation time τ, the characteristic time for a system to rearrange its structure on the length scale of its constituents. However, existing studies only probe length scales of the order of hundreds of nanometres, which are suitable for many soft materials, but are too large for molecular systems. A group of researchers have recently exploited the unique possibilities offered today by X-ray photon correlation spectroscopy (XPCS) [2] to follow the dynamics and the ageing in a metallic glass former at the atomic scale.
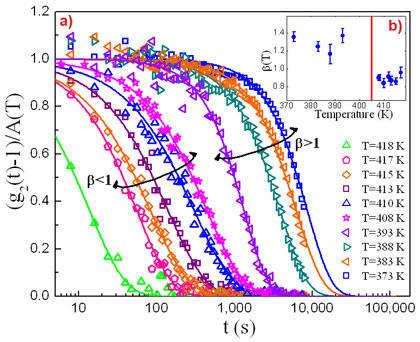
XPCS measurements were performed at beamline ID10 on a sample of Mg65Cu25Y10, in both the supercooled liquid and the glass state for different temperatures and thermal paths. Structural relaxation has been investigated by monitoring the decay of the intensity autocorrelation function g2(t). As shown in Figure 1, we find that the dynamics are not frozen in the glassy state and that the correlation functions display a full decay to zero, whose decay time τ increases with decreasing temperature. Thus, the system can rearrange its structure at the atomic length scale even if it is not at thermodynamic equilibrium. In fact, the curves in the glassy state depend on tw and thermal history, while the dynamics are stationary in the supercooled liquid. To compare different temperatures, it is therefore necessary to consider data taken in the glass at the same age, or waiting time from temperature equilibration. More surprisingly, we find a remarkable equilibrium/out-of-equilibrium dynamical crossover at the glass transition temperature Tg=405 K, signalled by a sharp change of the shape of the correlation functions, from stretched (β=0.88<1) in the supercooled liquid to “compressed” (β~1.3>1) in the glass.
While it is well known that the structural relaxation of supercooled liquids can be generally described by stretched exponential functions, the compressed behaviour found below Tg is totally unexpected and points to a different origin of the microscopic dynamics, unaccounted for in previous works. This behaviour can be explained in terms of internal stress relaxations as in the case of many out-of-equilibrium soft materials, such as concentrated colloidal suspensions and polymeric gels. Indeed, compressed correlation functions have been observed in these systems and have been associated with ballistic rather than diffusive motion due to internal stresses stored when the system is quenched in an out-of-equilibrium configuration [3]. The same explanation fits well also for metallic glasses. In fact, it is well-known that the extremely fast quenching used for their production leads to an excess of frozen-in free volume, because the melt does not have enough time to rearrange its structure into a more stable configuration before reaching the glassy state. Therefore, the glass contains internal stresses which are then released upon heating the system.
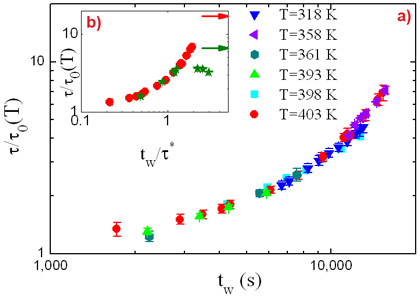
The similarity with out-of-equilibrium soft materials is further evidenced by looking at the evolution of the dynamics with ageing below Tg. We find that the glassy state is characterised by the presence of a complex hierarchy of ageing regimes which strongly resembles that reported for polymeric gels and clays. In particular, we find a fast, exponential growth of τ with waiting time for high cooling rates and short tw, followed by an almost frozen regime, where the evolution of the dynamics due to ageing takes too long with respect to our experimental time window (see Figure 2). In the first regime the growth rate does not depend on T and sets of data taken at the same T can be modelled by the empirical law
τ(T,tw)=τ0(T)exp(tw/τ*),
and rescaled onto a master curve by plotting τ/τ0 vs. tw (Figure 2a). The appearance of the second ageing regime requires sufficient annealing of internal stresses and depends on the previous thermal history (Figure 2b). These results obtained for a metallic glass point to stress relaxation as a universal mechanism driving the relaxation dynamics of out-of-equilibrium systems.
Principal publication and authors
B. Ruta (a), Y. Chushkin (a), G. Monaco (a), L. Cipelletti (b), E. Pineda (c), P. Bruna (c), V.M. Giordano (d), and M. Gonzalez-Silveira (e), Atomic-scale relaxation dynamics and aging in a metallic glass probed by X-ray photon correlation spectroscopy, Phys. Rev. Lett. 109, 165701 (2012).
(a) ESRF
(b) Laboratoire Charles Coulomb UMR 5221, Montpellier (France)
(c) Universitat Politècnica de Catalunya, Castelldefels (Spain)
(d) Université Claude Bernard Lyon 1 and CNRS, Lyon (France)
(e) Universitat Autònoma de Barcelona, Bellaterra (Spain)
References
[1] P.G. Debenedetti, and F.H. Stillinger, Nature 410, 259 (2001); L. Cipelletti, et al., Faraday Discuss. 123, 237 (2003).
[2] M. Leitner et al., Nat. Mat. 8, 717 (2009).
[3] J.P. Bouchaud, and E. Pitard, Eur. Phys. J. E 6, 231 (2001); L. Cipelletti, et al., Phys. Rev. Lett. 84, 2275 (2000).
Top image: Sample of metallic glass (Credit: E. Pineda and P. Bruna, Universitat Politècnica de Catalunya)