- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2017
- Complex systems and biomedical sciences
- Ultra-fast control of nanoscale deformations in solids
Ultra-fast control of nanoscale deformations in solids
The spatio-temporal coherent control of thermal excitations in solids has been demonstrated by intersecting a sequence of optical pulses on a sample surface. Deformation control can be employed for strain-induced applications in modern nanostructures.
Density changes in the crystal lattice of nanostructures lead to modifications of physical properties, e.g., band gap energy, magnetic anisotropies or electrical conductivity. Such density variations are generally described by lattice vibrations, so-called acoustic phonons that occur as incoherent or coherent superposition of modes. The former corresponds to a finite lattice temperature while the latter describes a sound wave with specific propagation speed and wave vector. Ultra-short laser pulses can generate coherent acoustic phonons on nanosecond length and picosecond timescales. Thus, they are ideal excitations for functionalisation of nanoscale systems.
At ID19, a new experimental method is presented that allows for full spatio-temporal control of the deformation, comprising both coherent acoustic sound waves and the incoherent thermal background. Using time-resolved X-ray reflectivity (TR-XRR), the absolute deformation amplitude u(t) of the surface is monitored with sub-Angstrom spatial and 100 ps temporal resolution.
As an example, a periodic surface modulation is generated by intersecting two femtosecond laser pulses that interfere on the sample surface. The sample is heated by the laser in the interference maxima and remains at the initial temperature in regions of destructive interference of the two pump pulses. On top of the thermal expansion, a surface modulation is generated by propagating surface sound waves, which are triggered by the impulsive optical excitation.
 |
|
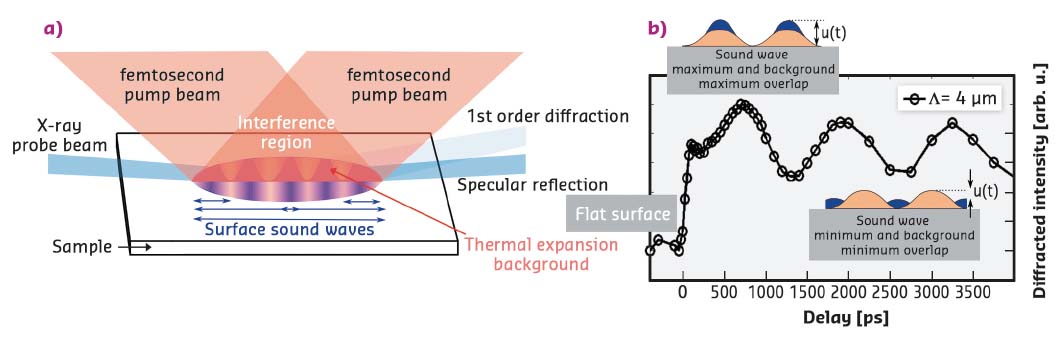
Fig. 64: a) Generation of a periodic surface modulation u(t) by intersecting two femtosecond laser pulses and probing by time-resolved X-ray reflectivity (TR-XRR). b) Intensity of the first diffraction order vs. time. The initial rise denotes the thermal background, the oscillation stems from propagating sound waves at the sample surface. |
The excursion at the surface is measured by TR-XRR as depicted in Figure 64a. Based on the experimental data in Figure 64b, a quadratic dependence of the 1st order diffracted X-ray intensity I(t) and the square of surface amplitude u(t) was derived, thus allowing for an absolute measurement of the deformation. Directly after the optical excitation, the diffracted intensity from the initially flat surface exhibits a step-like increase and subsequent oscillations. The oscillations stem from the modulation of the thermal background (orange) by propagating sound waves (blue) as depicted in the inset of Figure 64b.
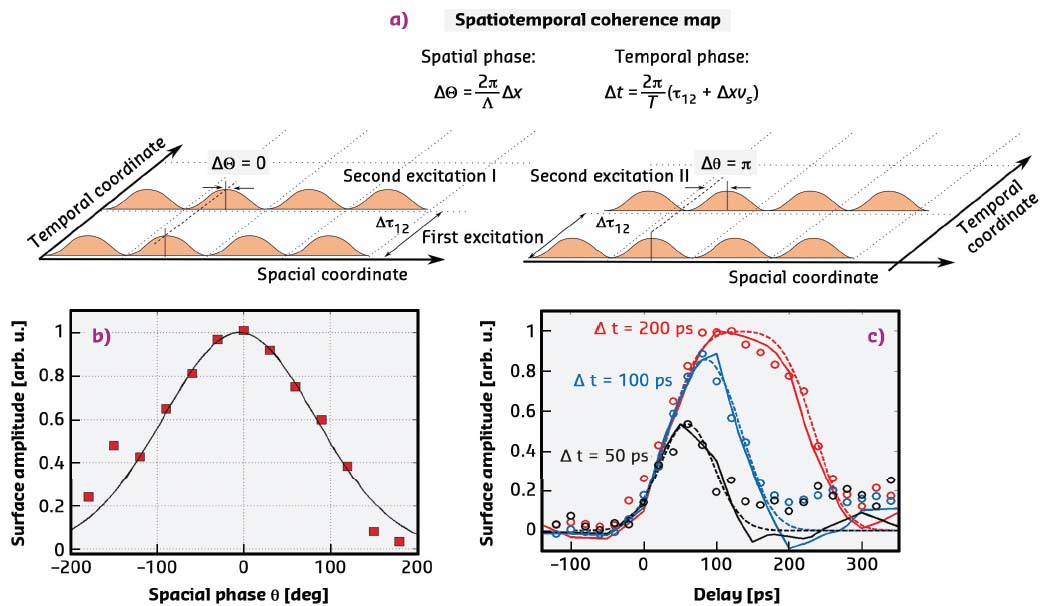
To demonstrate spatio-temporal strain control, the temporal and spatial coherence is exploited as explained in Figure 65a. A temporal sequence of excitation pulses is employed to control the amplitude of the sound wave at the sample surface. The incoherent thermal background is controlled via the spatial periodicity of the optical excitation. The first excitation defines spatial and temporal phase. A second excitation is either spatially in phase, as in Figure 65a (I), or out of phase (II). Only (II) removes the thermal grating, while (I) always amplifies the thermal background. However, both excitations may remove the coherent sound waves, depending on the relative temporal phase of the second excitation.
The experimental results are shown in Figure 65b and Figure 65c. The left panel depicts the variation of the spatial phase ∆θ in the range 0 – 2π, while the temporal phase is at ∆t ≈ 0. Variation of the spatial phase controls the diffracted 1st order intensity. Variation of the temporal phase ∆t is shown in Figure 65c while the spatial phase remains ∆θ = π. In particular, this measurement shows that thermal background and coherent excitation are suppressed by the second excitation.
 |
|
Fig. 65: a) Spatio-temporal coherence map for a spatial phase of ∆θ = 0 (left) and ∆θ = θ (right). b) and c) variation of the spatial and temporal phase, respectively. |
The data is the first demonstration of controlling the thermal and coherent strain in a nanostructure by a sequence of light pulses. Practical applications include employing surface deformations as control mechanisms for active X-ray optics. For example, the data in Figure 65c shows a switchable mirror that could be exploited as pulse picker or beam splitter in synchrotron applications. Other applications are generation and control of strain-induced processes in solid state magnetism, quantum computing or catalysis.
Principal publication and authors
Spatiotemporal Coherent Control of Thermal Excitations in Solids, M. Sander (a), M. Herzog (a), J. E. Pudell (a), M. Bargheer (a, b), N. Weinkauf (c), M. Pedersen (d), G. Newby (d), J. Sellmann (e), J. Schwarzkopf (e), V. Besse (f), V. V. Temnov (f, g) and P. Gaal (b, c), Phys. Rev. Lett. 119, 075901 (2017); doi: 10.1103/PhysRevLett.119.075901.
(a) Institute for Physics and Astronomy, Universität Potsdam (Germany)
(b) Helmholtz-Zentrum Berlin for Materials and Energy GmbH, Berlin (Germany)
(c) Institute for Solid State and Nanostructure Physics, Universität Hamburg (Germany)
(d) ESRF
(e) Institute for Crystal Growth, Berlin (Germany)
(f) IMMM CNRS 6283, Université du Maine, Le Mans (France)
(g) Groupe d’Etude de la Matière Condensée (GEMaC), Université de Versailles-Saint Quentin en Yvelines, CNRS UMR 8635, Université Paris-Saclay, Versailles (France)



