- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2016
- Matter at extremes
- Mott gap and magnetic interactions in NiO at ultra-high pressure
Mott gap and magnetic interactions in NiO at ultra-high pressure
Combined experimental and theoretical studies of NiO revealed the stability of its antiferromagnetic state up to 280 GPa and indicate the absence of a Mott transition to this pressure.
Many novel materials at the frontier of solid state physics are strongly correlated systems. They include high-Tc superconductors, Mott insulators, spintronic materials, ferroelectrics, and heavy fermion materials. In such materials, correlations between the more localised 3d or 4f electrons play a key role in determining the properties of the system.
NiO is considered one of the most important compounds for the field of strongly correlated materials for two reasons. Firstly, it was treated as a prototype by Mott to explain the nature of the insulating state that came to bear his name. Secondly, it is chemically a compound with a rather simple crystal structure and d8 electron configuration (i.e. lacking high-spin - low-spin transitions, Jahn-Teller effects, etc.) making it well suited to the experimental validation of theoretical models. Additionally, the absence of a spin-state degree in NiO is an advantage of the material as a system for investigations of insulator-to-metal transition (IMT) due to Mott or charge transfer gap closure compared to MnO, FeO or CoO. Futhermore, nothing other than a decrease of interatomic distances will affect the balance between charge transfer and Mott-Hubbard gap. Thus NiO is the only case where we may definitely observe the pure Mott type IMT and therefore determine its exact mechanism and effects on magnetic ordering and magnetic moment. The pressure of the IMT has been studied theoretically, with results ranging between 230 GPa [1] and 3.7 TPa [2]. Due to the many difficulties to conduct experiments at such ultra-high pressure, which drastically limit the number of available methods for measurements, the amount of experimental work on the actual IMT in NiO is scarce. However, the long-sought IMT in NiO was recently reported to be found at 240 GPa by resistivity measurements [3]. In all known cases, an IMT in a Mott insulator has been associated with the loss of magnetic order, and this is expected to apply to NiO as well [1]. Therefore, magnetic investigations are essential to understand the IMT in Mott insulators, as the disappearance of magnetic ordering is the only clear indication of the Mott type IMT.
 |
|
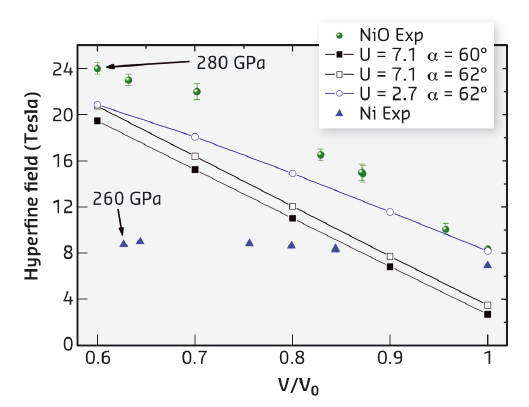
Fig. 139: Pressure dependence of the magnetic hyperfine field in NiO obtained by experiment and ab initio calculations (LSDA+U) within various approximations: filled olive circles - NiO by NFS, filled black squares by LSDA+U for U = 7.1 eV and αR = 60°, black squares by LSDA+U for U = 7.1 eV and α = 62°; blue circles by LSDA+U for U = 2.7 eV and α = 62°. Filled blue triangles represent the dependence of the magnetic hyperfine field in Ni by NFS from [5], given here for comparison. The lines are guides for the eye. |
We measured nuclear forward scattering (NFS) that was successfully applied to the Mössbauer transition of 61Ni [4,5] at beamline ID18, to perform an investigation of the magnetic properties of NiO at room temperature up to 280 GPa (Figure 139). We found that the antiferromagnetic order is preserved in the system up to at least 280 GPa, the highest pressure at which magnetism has been observed so far in any material. We complemented our magnetic ordering investigation by X-ray diffraction at beamline ID09A (now ID15B) and APS beamline 13IDD to 220 GPa and extended X-ray absorption fine structure (EXAFS) at beamline ID24 for structural investigations to 280 GPa. This is, to the best of our knowledge, the highest pressure at which an EXAFS spectrum has ever been collected. Neither technique indicates any change attributed to structural and/or electronic phase transitions up to the highest pressure achieved. These experimental observations are well reproduced by our ab initio calculations, which also yield a Mott insulator gap in the entire pressure range of this study. Our results thus indicate the absence of a Mott transition in NiO up to approximately 300 GPa. Thus additional experimental and theoretical investigations are necessary for this topic that everyone believed to be closed.
Principal publication and authors
Magnetic interactions in NiO at ultrahigh pressure, V. Potapkin (a), L. Dubrovinsky (b), I. Sergueev (c), M. Ekholm (d), I. Kantor (e), D. Bessas (e), E. Bykova (b), V. Prakapenka (f), R.P. Hermann (a,g), R. Rüffer (e), V. Cerantola (b), H.J.M. Jönsson (h), W. Olovsson (h), S. Mankovsky (i), H. Ebert (i) and I.A. Abrikosov (d,j,k), Physical Review B 93, 201110(R) (2016); doi: 10.1103/PhysRevB.93.201110.
(a) Jülich Centre for Neutron Science (JCNS) and Peter Grünberg Institut (PGI), JARA-FIT, Forschungszentrum Jülich GmbH, Jülich (Germany)
(b) Bayerisches Geoinstitut, Universität Bayreuth (Germany)
(c) Deutsches Elektronen-Synchrotron, Hamburg (Germany)
(d) Swedish e-Science Research Centre (SeRC), Department of Physics, Chemistry and Biology (IFM), Linköping University (Sweden)
(e) ESRF
(f) CARS, University of Chicago (USA)
(g) Materials Science and Technology Division, Oak Ridge National Laboratory (USA)
(h) Department of Physics, Chemistry and Biology (IFM), Linköping University (Sweden)
(i) Department of Chemistry, Ludwig-Maximilians-Universität München (Germany)
(j) Materials Modeling and Development Laboratory, National University of Science and Technology ‘MISIS’, Moscow (Russia)
(k) LACOMAS Laboratory, Tomsk State University (Russia)
References
[1] R.E. Cohen, Science 275, 654 (1997).
[2] X.-B. Feng and N.M. Harrison, Phys. Rev. B 69, 035114 (2004).
[3] A.G. Gavriliuk et al., Phys. Rev. Lett. 109, 086402 (2012).
[4] I. Sergueev et al., Phys. Rev. Lett. 99, 097601 (2007).
[5] I. Sergueev et al., Phys. Rev. Lett. 111, 157601 (2013).



