- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2016
- Enabling technologies
- Merging of synchrotron serial crystallographic data by a genetic algorithm
Merging of synchrotron serial crystallographic data by a genetic algorithm
A new method has been developed for the analysis of serial crystallographic data using a genetic algorithm.
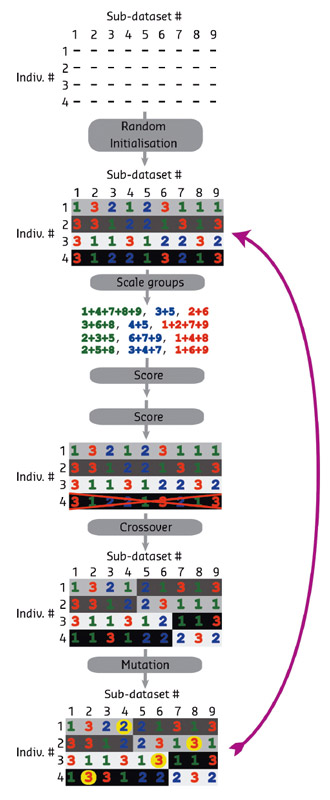
In the early days of macromolecular crystallography (MX), it was not uncommon to collect data from multiple crystals and merge them in order to obtain single, high quality datasets. It was quickly discovered, however, that non-isomorphism between crystals could be a severe limitation to this technique. In the ensuing years, advances in detectors, diffractometers, synchrotron beamlines and cryo-cooling, have made the collection of datasets from single crystals the standard for MX. Pioneering work at the ESRF at the ID13 beamline introduced a new twist: collecting multiple sub-datasets from a single crystal [1]. Multi-crystal and multi-position data collection strategies are referred to as serial crystallography (SX) and have seen an enormous upswing in interest, largely spurred by successes at the LCLS and SACLA free electron lasers [2,3]. Recently, some FEL sample delivery and data analysis methods have been adapted and extended for use at synchrotron sources at both cryogenic and ambient temperatures [4,5]. One particularly exciting adaptation of SX is a cryogenic method that takes advantage of the ability to collect small oscillation ranges from multiple crystals [6]. However, the problem of dealing with non-isomorphism has again entered the limelight. The degree of non-isomorphism is dependent on many factors, including the inherent differences between the crystals as well as changes induced by crystal handling (dehydration, for example). To address this challenge, hierarchical cluster analysis (HCA) has been the method of choice to date. Specifically, HCA is used to construct a "family tree" of a population of datasets, which can then be used as a guide to select which "branches" can be merged. This method uses metrics of similarity between datasets, most notably correlation coefficients between intensities, similarity of unit cell parameters and relative correlation of intensities in anomalous pairs [7–9]. With the exception of the latter, these values are a proxy for the presumed data quality of the merged data, which is a severe limitation of this methodology. We have therefore chosen to use merged data quality, in particular data metrics such as R values CC1/2 and <I/sig(I)>, as a guide for selecting merging groups. If the number of sub-datasets is very small, all possible combinations of subsets can be evaluated. However, for a set of n sub–datasets, the number of possible combinations is 2n-1, thus an exhaustive search quickly becomes computationally unfeasible even with relatively few sub-datasets. To address this problem, we have therefore used global optimisation as a means of identifying sets of sub-datasets that can be merged with good statistics. Genetic algorithms (GAs) are a well known global optimisation method. In this work we show that a GA (Figures 156, 157) can be used to select which sub-datasets can be merged into a high quality dataset. We show that for data from well-known test systems such as thermolysin, insulin and glucose isomerase, improvements to data quality can be made, as assessed by both merging statistics and paired refinements. We furthermore show that similar improvements can be seen even for a difficult low symmetry test case with very poor diffraction limits.
 |
|
Fig. 156: Graphical representation of the optimisation of merging datsets by a genetic algorithm. Early generations appear at the top of the image and the last generations appear at the bottom. The fitness (darker colours) is improved at each generation. |
Principal publication and authors
Merging of synchrotron serial crystallographic data by a genetic algorithm, U. Zander (a), M. Cianci (b), N. Foos (a), C.S. Silva (c), L. Mazzei (d), C. Zubieta (c), A. de Maria (a) and M.H. Nanao (a,e), Acta Cryst. D72, 1026–1035 (2016); doi: 10.1107/S2059798316012079.
(a) ESRF
(b) European Molecular Biology Laboratory, Hamburg Outstation, c/o DESY, Hamburg (Germany)
(c) Laboratoire de Physiologie Cellulaire & Végétale, Univ. Grenoble Alpes, CNRS, CEA, INRA, BIG, Grenoble (France)
(d) Laboratory of Bioinorganic Chemistry, Department of Pharmacy and Biotechnology, University of Bologna (Italy)
(e) EMBL Grenoble (France)
References
[1] A. Perrakis et al., Acta Cryst. D55, 1765–70 (1999).
[2] S. Boutet et al., Science 337, 362–4 (2012).
[3] H.N. Chapman, Synchrotron Radiat News 28, 20–4 (2015).
[4] C. Gati et al., IUCrJ. 1, 87–94 (2014).
[5] F. Stellato et al., IUCrJ. 1, 204–12 (2014).
[6] U. Zander et al., Acta Cryst. D71, 2328–43 (2015).
[7] R. Giordano et al., Acta Cryst. D68, 649–58 (2012).
[8] Q. Liu et al., Science 336, 1033–7 (2012).
[9] J. Foadi et al., Acta Cryst. D69, 1617–32 (2014).