- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2015
- Matter at extremes
- High Poisson’s ratio of Earth’s inner core explained by carbon alloying
High Poisson’s ratio of Earth’s inner core explained by carbon alloying
The behaviour of Fe7C3 was investigated up to pressure conditions of the Earth’s core using X-ray diffraction, Mössbauer spectroscopy and nuclear inelastic scattering. These experiments revealed that the anomalous elastic properties of the Earth’s inner core found by seismology may be explained by the presence of carbon as an alloying light element.
Most of our knowledge of the Earth’s deep interior comes from comparison of laboratory measurements of physical properties of materials with data from bulk geophysical methods. In particular, seismology has been the traditional method for providing constraints on the physics of the Earth’s interior. Seismology provides three independent physical parameters: density and compressional and shear sound wave velocities. Combining these constraints with geochemical and cosmochemical considerations, available data suggests that iron (or iron–nickel alloy) is the main component of the Earth’s core. However, a large inconsistency still exists between the density of pure iron at pressure and temperature conditions of the Earth’s core and seismological estimates, which can only be explained by the presence of light elements such as oxygen, silicon, sulfur, hydrogen or carbon. In addition, the low shear wave velocity and high Poisson’s ratio of the Earth’s core remains enigmatic. None of the available mineral physics data of light element bearing Fe alloys can explain the rubber like Poisson’s ratio (0.45) present in the Earth’s core.
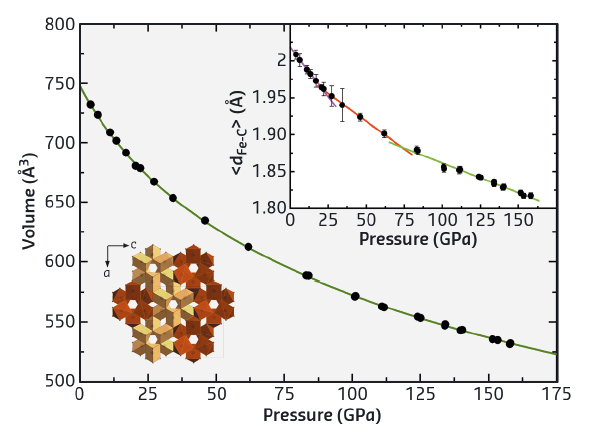 |
|
Fig. 100: Volume–pressure data for Fe7C3 with the fitted third-order Birch–Murnaghan equation of state (K300 = 168(4) GPa, K’ = 6.1(1)). The upper inset shows the variation of mean carbon to iron distances, <dFe-C> in Fe7C3 with pressure, whereby the data show three linear regions with transitions around 16 GPa and 70 GPa, marking the ferromagnetic to paramagnetic and paramagnetic to non-magnetic transitions, respectively (further details are given in the text). The lower left inset shows a polyhedral model of the crystal structure of Fe7C3 projected in the b-direction. |
In this study, we investigated the magnetic and elastic properties of Fe7C3 up to core conditions. Carbon is a plausible light element in the Earth’s core and estimates based on current available data suggest that 1.1wt% of carbon may be present in the Earth’s inner core. The equation of state (EOS) of single crystal Fe7C3 was measured up to 156 GPa using the unique capabilities of X-ray diffraction beamline ID09, now ID15B, (Figure 100), which provides a small and intense beam and is equipped with a fast large area X-ray detector. The methodology and strategy for data collection was developed in collaboration between ESRF and Bayreuth scientists, allowing the range for single crystal diffraction experiments (structure solution and refinement) to be extended to pressures of the Earth’s core. The novel synchrotron Mössbauer source (SMS) developed at ID18 was used to investigate the electronic properties of Fe7C3 up to 132 GPa and nuclear inelastic scattering (NIS) was measured at ID18 in order to obtain elastic properties up to 158 GPa, which was made possible by the recently improved capabilities including decreased X-ray beam size and better energy resolution. We found that Fe7C3 undergoes two magnetic transitions, a ferromagnetic to paramagnetic transition at about 16 GPa and a paramagnetic to nonmagnetic transition at about 70 GPa. The EOS seems not to be affected by these transitions, only the mean Fe-C distances show an accompanying change in slope with pressure (Figure 100). By combining the EOS and NIS results, we obtained density, shear sound wave velocity and compressional sound wave velocity of Fe7C3 up to core conditions. Estimated extrapolated shear wave and compressional wave velocities show that Fe7C3 exhibits a lower shear wave velocity than pure iron and a Poisson’s ratio similar to that of the Earth’s inner core (Figure 101). We suggest that carbon alloying significantly modifies the properties of iron at extreme conditions to approach the elastic behaviour of rubber. Thus, the presence of carbon may explain the anomalous elastic properties of the Earth’s core.
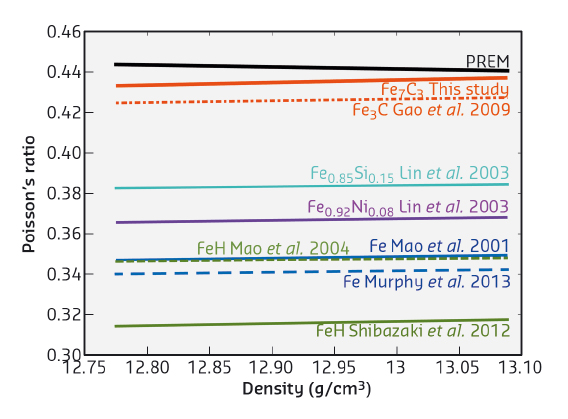 |
|
Fig. 101: Extrapolation of Poisson’s ratio to the densities estimated in the Earth’s inner core using Birch’s law [1-7]. The only element which significantly increases the Poisson’s ratio of iron is carbon. Moreover, the estimated Poisson’s ratio of Fe7C3 nearly approaches the Poisson’s ratio of the preliminary Earth reference model (PREM [7]) at densities near the centre of the inner core. |
Principal publication and authors
High Poisson’s ratio of Earth’s inner core explained by carbon alloying, C. Prescher (a,b), L. Dubrovinsky (a), E. Bykova (a,c), I. Kupenko (a,d), K. Glazyrin (a,e), A. Kantor (a,d), C. McCammon (a), M. Mookherjee (a,f), Y. Nakajima (a,g), N. Miyajima (a), R. Sinmyo (a), V. Cerantola (a), N. Dubrovinskaia (c), V. Prakapenka (b), R. Rüffer (d), A. Chumakov (d,h) and M. Hanfland (d), Nature Geoscience 8, 220-223 (2015); doi: 10.1038/NGEO2370.
(a) Bayerisches Geoinstitut, Universität Bayreuth (Germany)
(b) Center for Advanced Radiation Sources, University of Chicago (USA)
(c) Laboratory of Crystallography, Material Physics and Technology at Extreme Conditions, University of Bayreuth (Germany)
(d) ESRF
(e) Petra III, P02, Deutsches Elektronen Synchrotron, Hamburg (Germany)
(f) Earth and Atmospheric Sciences, Cornell University (USA)
(g) Materials Dynamics Laboratory, RIKEN Spring-8 Center, Hyogo (Japan)
(h) National Research Center “Kurchatov Institut”, Moscow (Russia)
References
[1] L. Gao et al., Geophys. Res. Lett. 35, 1 (2008).
[2] J.-F. Lin et al., Geophys. Res. Lett. 30, 2112 (2003).
[3] H.K. Mao et al., Science 292, 914 (2001).
[4] W.L. Mao et al., Phys. Res. Lett. 31, L15618 (2004).
[5] C.A. Murphy et al., J. Geophys. Res. B 118, 1999 (2013).
[6] Y. Shibazaki et al., Earth Planet. Sci. Lett. 313-314, 79 (2012).
[7] A.D. Dziewonski and D.L. Anderson, Phys. Earth Planet. Inter. 25, 297 (1981).



