- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2015
- Electronic structure, magnetism and dynamics
- Correlation of ground state properties and orbital anisotropy in heavy fermion materials
Correlation of ground state properties and orbital anisotropy in heavy fermion materials
The interplay of structural, orbital, charge, and spin degrees of freedom is at the heart of many physical phenomena, including superconductivity. Unraveling the underlying forces requires an understanding of each of these degrees of freedom as well as the interplay between them. Cerium-based heavy fermion compounds are an ideal playground for investigating these interdependencies, and a correlation between the orbital anisotropy and the ground states in a representative family of materials has been shown.
The detailed mechanism of high-temperature superconductivity is not yet understood, neither in the copper oxide nor in the Fe-pnictide high-temperature superconductors. It is believed though, that the interplay of magnetism and superconductivity is of central importance. Here, the so called heavy fermion compounds enter the stage. They are conducting materials where the charge carriers move as if their mass were 1000 times heavier than the mass of the free electron and for this reason they are called heavy fermions. This mass enhancement originates from strong interactions between electrons. The heavy fermion phenomenon can be found in many solids containing cerium (Ce) or ytterbium (Yb). Many heavy fermion compounds also exhibit unconventional superconductivity, therefore, we should gain new insights into the mechanism of high-temperature superconductivity if we could understand heavy fermion phase diagrams.
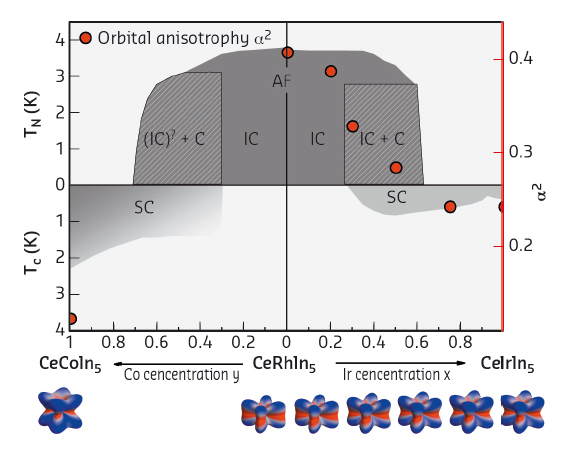
The members of the heavy fermion family CeMIn5 with M = Co, Rh or Ir exhibit superconducting and magnetic ground states when substituting one M element for another (see Figure 50) [1]. These materials are therefore recognised as important model systems in which a search for parameters that correlate with the formation of a magnetic or superconducting ground state could be successful.
 |
|
Fig. 50: Substitution phase diagram of CeMIn5 compounds; SC stands for superconducting and AF for antiferromagnetic. The dots are the orbital anisotropy α2 as a function of x for CeRh1–xIrxIn5 and for CeCoIn5 with the scale on the right hand side. The respective angular distributions of the 4f CEF ground-state orbitals in CeRh1–xIrxIn5 and CeCoIn5 is shown below the phase diagram. |
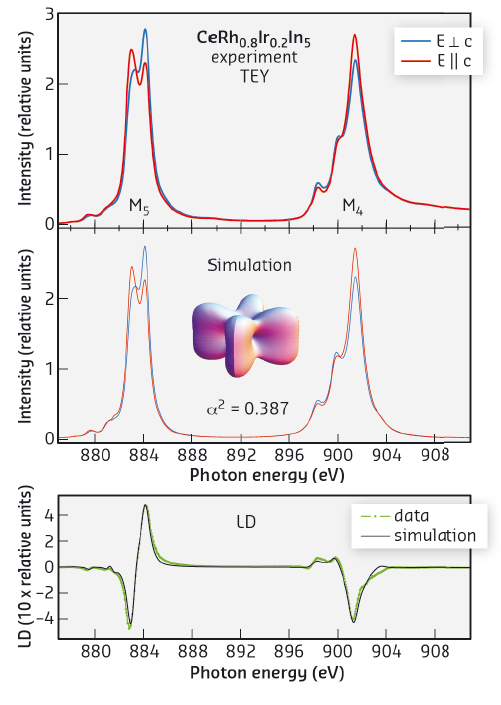
Here we investigated the 4f crystal-electric field ground-state wave functions of the strongly correlated materials CeRh1–xIrxIn5 across the phase diagram (see Figure 50). The ground state wave functions were measured with great accuracy using linear polarisation-dependent soft X-ray absorption spectroscopy (XAS) at the cerium M-edges (see top of Figure 51). To assure that only the ground state was probed, the measurements were performed at low temperature. The data were analysed with a full multiplet routine including a crystal-field model (see middle and bottom of Figure 51), and a ground state wave function of the type
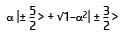
 |
|
Fig. 51: Measured M-edge of CeRh0.8Ir0.2In5 for linear polarised light. Middle: simulation with the full multiplet routine including the crystal-field model. Bottom: experimental and simulated linear dichroism. |
was assigned to each Ir concentration. Here α, which stands for the amount of Jz = 5/2 and 3/2 in the ground state, determines the shape of the orbitals. The wave functions of the full compounds were determined in an earlier experiment [2]. We found that the parameter a scales very sensitively with the respective ground state (see red dots in Figure 50) such that flatter orbitals correlate with magnetic order, while more extended orbitals occur in the superconducting compositions (see Figure 50). The more extended orbitals can intermix (hybridise) more easily with other electrons and therefore contribute more to the electric conductivity. These observations are independent of lattice effects. Such a correlation had been theoretically suspected, but it was only now proven experimentally thanks to these polarised X-ray absorption measurements at beamline ID08 (now ID32).
Our results yield a microscopic picture of these materials as they become superconducting; this will hopefully stimulate further theoretical descriptions.
Principal publication and authors
Correlation between ground state and orbital anisotropy in heavy fermion materials, T. Willers (a), F. Strigari (a), Z. Hu (b), V. Sessi (c), N.B. Brookes (c), E.D. Bauer (d), J.L. Sarrao (d), J.D. Thompson (d), A. Tanaka (e), S. Wirth (b), L.H. Tjeng (b) and A. Severing (a), PNAS 112, 2384, (2015); doi: 10.1073/pnas.1415657112.
(a) Institute of Physics II, University of Cologne (Germany)
(b) Max Planck Institute for Chemical Physics of Solids, Dresden (Germany)
(c) ESRF
(d) Los Alamos National Laboratory (USA)
(e) Hiroshima University (Japan)
References
[1] J.D. Thompson and Z. Fisk, J. Phys. Soc. Jpn. 81, 011002 (2012), and references therein.
[2] T. Willers et al., Phys. Rev. B 81, 195114 (2010).



