- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2014
- Dynamics and extreme conditions
- Giant pressure-induced volume collapse in the pyrite mineral MnS2
Giant pressure-induced volume collapse in the pyrite mineral MnS2
Magnetism plays an important role in determining the properties of the minerals that make up Earth’s crust and mantle [1]. This is due to the ubiquity of transition metals (notably Fe) with unpaired electrons. Under geological pressures, these may undergo abrupt volume collapses due to spin-state transitions, where the number of unpaired electrons is sharply reduced. This occurs when the crystal field splitting Δ, competes with Hund’s rule and electronic Coulomb repulsion to determine the size of the magnetic moment. High pressure can thus make a high-spin (e.g., S = 5/2) state unstable with respect to a low-spin state (e.g. S = 1/2). The primary driving force for this effect is an increase in Δ as the metal–ligand bond distances decrease. Many simple materials show pressure-induced spin state transitions, and volume collapses of ΔV ≈ 5% are regarded as notable. Understanding the mechanisms of such magnetically driven transitions, and predicting the high-pressure structures, is ultimately of great importance for modelling the Earth›s mantle in particular.
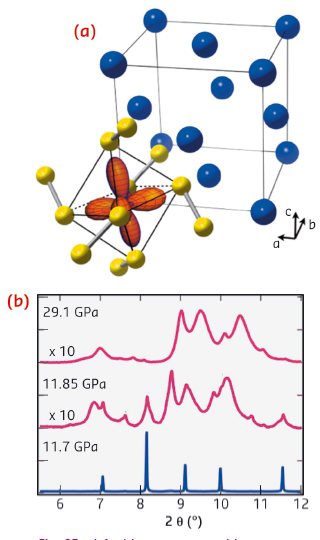 |
|
Fig. 92: a) Ambient pressure cubic structure of MnS2, showing the fcc lattice of Mn sites (blue) and highlighting the valence eg orbitals of one cation. b) Pressure dependence of diffraction data (ID09A) through the volume collapse, showing the formation of a disordered intermediate. |
Using diamond anvil cells at ID09A and ID27, we discovered that a simple cubic manganese mineral (Hauerite, MnS2) undergoes a truly giant 22% shrinkage of unit cell volume above 12 GPa. Instead of the expected transition between crystalline high and low-spin phases, compression induces the formation of a disordered intermediate (Figure 92). As we were unable to solve the high pressure structure from this data, we made use of recently developed ab initio structure searching methods implemented in the USPEX package [2], which predicted a new monoclinic polymorph. Using the recently commissioned online CO2 laser heating at ID27, we were able to recrystallise the sample at 20 GPa. Indexing and Rietveld refinement confirmed the predicted structure (Figure 93). This contains a notable distortion, with neighbouring Mn atoms forming short bonds along one-dimensional chains of edge-sharing MnS6 octahedra. Density functional theory calculations show that this structure is low spin S = 1/2, and that the remaining spin per site is occupied in chemical bonding. Magnetism is thus completely quenched in this phase.
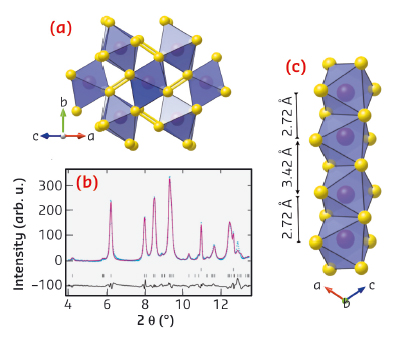 |
|
Fig. 93: a) High-pressure structure of MnS2 as predicted using USPEX and as refined against the ID27 diffraction data shown in b) at 20 GPa after laser heating. c) Perspective view of the high pressure structure showing the formation of short dimer bonds between neighbouring Mn cations in the edge-sharing chains. This viewpoint is perpendicular to that shown in a). |
Not only is the size of the volume collapse in MnS2 much larger than that found in other minerals, it therefore also occurs by a new mechanism. Traditionally, the electronic and magnetic properties of oxides and sulphides have been explained using a so-called ‘single-ion’ model [3]. This takes into account the spin, charge and orbital degeneracies of isolated cations. The results presented here go beyond this simple picture, and show that molecule-like units can spontaneously emerge under pressure in otherwise ordinary continuous lattice materials. In MnS2, the unpaired electrons on neighbouring cations form chemically bonded dimers, and it is this ‘squeezing out’ of magnetism which stabilises the giant increase in density of the new phase. Although its scarcity means that MnS2 is geologically insignificant, similar phenomena might be found in more abundant minerals containing iso-electronic cations such as Fe3+.
Principal publication and authors
S.A.J. Kimber (a), A. Salamat (a,b), S.R. Evans (a,c), H.O. Jeschke (d), K. Muthukumar (d), M. Tomic (d), F. Salvat-Pujol (d), R. Valenti (d), M.V. Kaisheva (e), I. Zizak (f) and T. Chatterji (g), Proc. Nat. Acad. Sci., 111, 5106 (2014).
(a) ESRF
(b) Lyman Laboratory of Physics, Harvard University, Cambridge (USA)
(c) Departement für Chemie und Biochemie, Universität Bern (Switzerland)
(d) Institut für Theoretische Physik, Goethe-Universität Frankfurt, Frankfurt am Main (Germany)
(e) School of Chemistry, University of Edinburgh (UK)
(f) Helmholtz-Zentrum Berlin für Materialien und Energie, Berliner Elektronenspeicherring-Gesellschaft für Synchrotronstrahlung-II, Berlin (Germany)
(g) Institut Max von Laue-Paul Langevin, Grenoble (France)
References
[1] R.E. Cohen, I.I. Mazin, Science, 275, 654 (1997).
[2] C.W. Glass, A.R. Oganov and N. Hansen, Comput. Phys. Commun, 175, 713 (2006).
[3] J.B. Goodenough, Phys. Rev., 100, 564 (1955).



