- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2013
- Electronic structure and magnetism
- Inside a ferrimagnet: probing magnetic sublattice reorientation at high magnetic field
Inside a ferrimagnet: probing magnetic sublattice reorientation at high magnetic field
Ferrimagnets are materials composed of different magnetic constituents. These may be different sites occupied by the same element, different elements or combinations thereof. Examples range from magnetite as one of the earliest known magnetic materials, to rare-earth transition-metal intermetallics which are of interest in the quest for hard magnetic materials, and double perovskites with characteristics making them candidates for spintronics applications. The strength of the magnetic interactions is determined by electronic and structural properties. The equivalent molecular fields can be very high, therefore one often needs equally high magnetic fields to explore their magnetic phase diagrams. Probing the behaviour of the individual constituents has remained challenging today and requires isotope-, site-, element- and orbital specific probes, offered by various X-ray techniques, - in high fields. Here, we used Fe K-edge XMCD in fields up to 30 T to probe the Fe magnetisation in the ferrimagnetic garnet Er3Fe5O12.
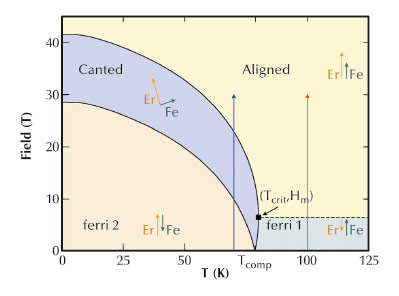
In the rare earth iron garnets, the magnetic ions are located at the centres of oxygen polyhedra with different symmetries. The exchange interactions over the oxygen atoms at the vertices lead to ferrimagnetic behaviour on two very different scales: On one side, the coupling between the two octahedral and three tetrahedral Fe sites is very strong and the antiferromagnetic alignment is only broken at the Curie temperature of 560 K or in excessively high fields. On the other side, the interaction of the Er ions with the unbalanced Fe net moment is much weaker, yet still requires applied fields of the order of tens of Tesla to compete with the molecular fields. Figure 102 shows the phase diagram of a simplified isotropic two sublattice model for the interaction of Er ions with the Fe-net moment. At high temperatures, the Er behaves like a paramagnet, polarised by the net Fe moment. With decreasing temperature, the Fe and the Er sublattices reverse orientation with respect to an applied field at the compensation temperature Tcomp = 78.8 K, where the Er magnetisation outweighs that of the Fe sites. However, the most intriguing manifestation of the different interactions becomes apparent in the field dependence of the Fe sublattice magnetisation. In our experiment, we used a miniature pulsed magnet system to reach 30 T and energy dispersive XMCD at ID24, that has an intrinsically simultaneous acquisition scheme, particularly suitable for differential experiments in time varying fields.
 |
|
Fig. 102: Isotropic two sublattice model for the phase diagram of Er3Fe5O12. Above the critical temperature, the Er sublattices behave as a paramagnet whose field dependence is offset through the molecular field created by the net moment of the Fe ions. A canted phase, bounded by second order transitions (solid lines) emerges below the critical temperature for the ordering of the Er ions. The red and blue arrows represent the field dependences shown in Figure 103. |
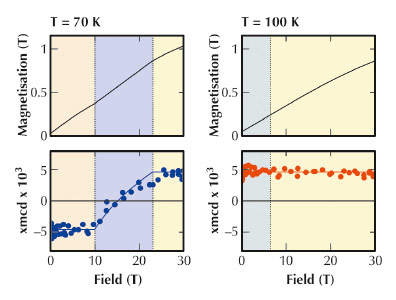
Above Tcrit, (Figure 102, red arrow) the Er ions first become thermally demagnetised when the applied field compensates the molecular field from the Fe sublattice (dashed line) and eventually becomes aligned with the Fe and the applied field. While the bulk magnetisation rises continuously, XMCD reveals that the Fe-sublattice magnetisation remains independent of the applied field up to 30 T (Figure 103, right panels). Below Tcrit, (Figure 102, blue arrow) the applied field gradually increases the Er magnetisation. When it matches the difference between the molecular fields of the Fe- and the Er sublattices, the Fe sublattice starts to rotate continuously, reversing by 180 degrees to align with the applied field after which it remains saturated again (Figure 103, left panels). Bounded by second order transitions, this canted phase remains barely visible in the bulk magnetisation, which grows continuously. The Fe-K edge XMCD (Figure 103, left panels) clearly shows first the opposite configuration, then the complete reversal within the canted phase, and finally the alignment with the applied field.
 |
|
Fig. 103: Calculated bulk magnetisation (top) and Fe K-edge XMCD (bottom) below and above the critical temperature. The bulk magnetisation rises continuously at both temperatures. The XMCD shows that the net magnetisation of the Fe sublattices remains saturated and aligned with the applied field at 100 K. At 70 K, it is opposite to the applied field and reverses continuously in the canted phase. |
In conclusion, we have used energy dispersive XMCD in pulsed high magnetic fields at the Fe-K-edge to probe the Fe-sublattice magnetisation in ferrimagnetic Er3Fe5O12. The field independent parts of the Fe magnetisation indicate the strong interaction between the tetrahedral and octahedral sites, whereas the continuous reorientation in the canted phase is the signature of the weak coupling of the Er sublattice to the Fe net moment.
Principal publication and authors
C. Strohm (a), T. Roth (a), C. Detlefs (a), P. van der Linden (a) and O. Mathon (a), Physical Review B 86, 214421 (2012).
(a) ESRF



