- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2013
- Dynamics and extreme conditions
- Does nuclear resonant scattering violate reciprocity?
Does nuclear resonant scattering violate reciprocity?
Newton’s third law has stated the equality of action and reaction between mechanical bodies. In the nineteenth century, von Helmholtz, Rayleigh and others formulated an analogy for classical waves, the reciprocity principle. According to this principle, the source and the detector can be interchanged without any consequence on the waves regardless of where the surrounding objects are located.
A number of physical phenomena can be described by scattering of waves. The signal observed in a scattering experiment is similarly expected to remain unchanged upon reversing the source and the detector. This often fulfilled expectation of the reciprocity principle has been generalised for more complex scattering systems, and, indeed, strict reciprocity theorems were formulated for specific cases. Reciprocity-related publications span the twentieth century, as summarised in the review of Potton [1]. Surprisingly, it turns out that the reciprocity principle does not actually follow from first principles of physics. Although obedience of the reciprocity principle was used in the antenna theory of radio communications in the early twentieth century, its violation in other areas of wave propagation is commonplace. Nowadays non-reciprocal devices such as circulators and isolators are routinely used in microwave and laser optics.
What then is reciprocity? In many studies, it is simply identified as time reversal symmetry. However, in polarisation-independent optics, absorption is known to violate time reversal symmetry, while reciprocity is obeyed. Similarly, the requirement of invariance upon interchanging the source and the detector, reciprocity is conjectured to be identical with a 180° rotation. However, this latter also fails, since there exist examples with no 180° rotational symmetry still obeying the reciprocity principle. Reciprocity, therefore, is neither a mere time-reversal, nor a mere 180° rotational invariance, but it is a special symmetry of the scattering amplitude, as explained in a recent theory of ours [2].
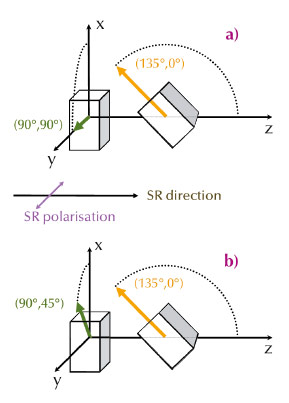
We studied the conditions of a system to obey or violate the reciprocity principle. Our aim was to select an experiment in which reciprocity violation is markedly strong, in order to unquestionably demonstrate whether reciprocity is obeyed or violated in a particular scattering experiment. To this end, nuclear resonant scattering (NRS) of synchrotron radiation was applied at the nuclear resonance side station ID22N in two experimental arrangements for ferromagnetic scatterers. Both scattering arrangements, cases shown in Figures 43a and 43b, consisted of two 6 m thick 57Fe foils uniformly magnetised in the plane of the foils in a magnetic field of 0.19 T. The z-axis was in the direction of the beam and the y-axis aligned with its linear polarisation. The spectra of the scatterers were compared to their reciprocal counterparts. The interchange of the source and the detector was realised by a 180° rotation of the entire sample holder around the x-axis [2].
 |
|
Fig. 43: Geometrical arrangement for a) the reciprocity-obeying and b) the reciprocity-violating case, respectively. The coloured arrows indicate the direction of the magnetic fields. |
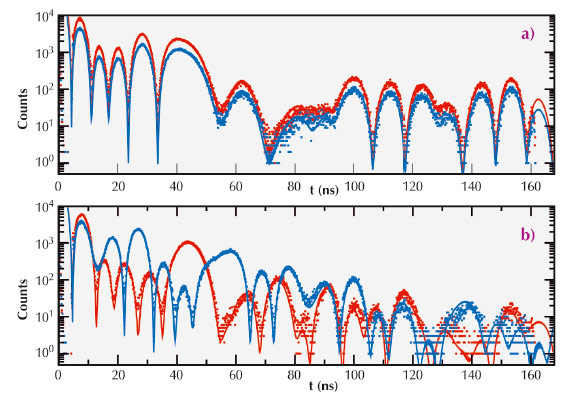
In a typical NRS experiment, the time response of the scatterer to the excitation by a synchrotron pulse is recorded and analysed. The synchrotron radiation pulse excites the hyperfine-split nuclear energy levels simultaneously, leading to characteristic beats in the time spectra. The four time spectra and the corresponding computer simulations are shown in Figure 44. The scattering arrangements in Figure 43 exhibit neither time reversal nor 180° rotational invariance around the x-axis. Our NRS experiments prove that the arrangement in Figure 43a results in obeying reciprocity in the measured intensities in Figure 44a, while the arrangement in Figure 43b exhibits apparent non-reciprocity in Figure 44b. When compared to earlier trials of experimental proof of non-reciprocity, this finding is exceptional due to the huge non-reciprocity. In certain time intervals, intensities in the direct and reciprocal scattering cases of Figure 44b differ as much as a factor of one thousand, while on switching back to arrangement Figure 43a, the intensities display full reciprocity in Figure 44a. (The difference of the spectra in Figure 44a is merely due to the difference in the total acquisition time.)
 |
|
Fig. 44: a) Measured and simulated NRS time spectra for the case displayed in Figure 43a in direct (red colour) and reciprocal (blue colour) geometry. b) Experimental data and simulations for the case shown in Figure 43b in direct and reciprocal geometry. |
In full agreement with theoretical expectations [2], it has therefore been undoubtedly demonstrated that the magneto-optic Faraday effect does not automatically give rise to non-reciprocity. Applications of switchable non-reciprocity are expected in the field of gamma-optics.
Principal publication and authors
L. Deák (a), L. Bottyán (a), T. Fülöp (a), G. Kertész (a), D.L. Nagy (a), R. Rüffer (b), H. Spiering (c), F. Tanczikó (a) and G. Vankó (a), Phys. Rev. Lett. 109, 237402 (2012).
(a) Wigner Research Centre for Physics, Budapest (Hungary)
(b) ESRF
(c) Johannes Gutenberg Universität, Mainz (Germany)
References
[1] R.J. Potton, Rep. Prog. Phys. 67, 717-753 (2004).
[2] L. Deák and T. Fülöp, Ann. Phys. (Amsterdam) 327, 1050-1077 (2012).



