Solution Uniqueness and Uniqueness Criteria

In general we are trying to obtain some values which characterise some system, often a physical system. However, evidence of those values is often available through indirect measurements i.e. our data values, and those values invariably have associated uncertainties e.g. due to counting statistics and electronic noise in detectors. It is often the case that the process leading to the measurable values involves a loss of information e.g. the point spread function in a positive sensitive detector. It can also be the case that important ``measurable'' values are not available owing to limitations in the experiment. This is termed ``missing data''. These three effects mean that invariably there are many possible sets of values which are consistent with the observed data values. These are ``lack of uniqueness'' problems.

Given such a problem it is reasonable to ask what are the properties of the different solutions and whether a particular solution can be taken with particular properties. One highly reasonable criterion used to choose a single solution, a uniqueness criterion, is the maximum likelihood method (MLM) i.e. Given the observed data and everything we know concerning the experiment which led to the recorded results; the most likely solution. A very simple example of the the MLM is the estimation of single value from a set of measurements of that value. If the measured values have some variation, and there is no reason to think that any one measurement is more or less accurate than any others, the MLM solution is just the average of the measured values. This is also a simple example of unweighted estimation. If, however, the measurements or data values are not considered to be of equal accuracy, then this needs to be taken into account and ``weighted'' estimation is performed. Ideally this would use full knowledge of the probability distributions of the measurement processes to assess the likelihood that the observed data could have been produced by a particular parameter value. The parameter value with the highest probability of producing the observed data is the maximum likelihood solution.

When data values are obtained with known Gaussian error distributions the MLM is strictly equivalent to least squares method i.e. our MLM objective function $f({\bf d, v, m})$ equals:

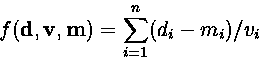$$f({\bf d, v, m}) = \sum_{i=1}^{n} (d_i - m_i) / v_i$$ (3)

where d_i is the measured value of data point i, m_i is the corresponding value calculated from the model, and v_i is the variance of the data point.

The error estimates are often not Gaussian, but more seriously they are invariably unknown, and poorly estimated (Schwarzenbach et al., 1989). For counting statistics data this poor estimation has been shown to be more important than the difference between the Poissonian and Gaussian error distributions, even for low count rates, and a simple method for largely reducing the introduced bias has been demonstrated (Hammersley & Antoniadis, 1997).

In FIT2D both unweighted and weighted least squares fitting may be performed (provided error estimates exist), and the weighted least squares fitting may be modified to ensure very good approximation to the MLM even for data with low counts and highly non-Gaussian Poisson distributed errors.