- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2009
- Dynamics and extreme conditions
- Breakdown of the continuum elasticity theory in glasses on the nanometric length-scale
Breakdown of the continuum elasticity theory in glasses on the nanometric length-scale
The thermal properties of insulating crystals at low-temperature are governed by low-frequency acoustic excitations. These can be understood using a simple continuum elasticity theory – the Debye model – and are characterised by a linear dispersion relation: their characteristic frequency is proportional to the wavenumber, the proportionality constant being the sound velocity. Compared to crystals, glasses display a set of anomalous universal low-temperature properties [1]. In particular, at a temperature (T) of ~10 K, the thermal conductivity shows a plateau and the specific heat is characterised by an excess over the ![]() T3 prediction of the Debye model. This excess is related to the so-called boson peak, an excess in the number of vibrational modes in the THz frequency (
T3 prediction of the Debye model. This excess is related to the so-called boson peak, an excess in the number of vibrational modes in the THz frequency (![]() ) range with respect to the
) range with respect to the ![]()
![]() 2 prediction of the Debye model. The physical origin of these universal properties has been lively discussed in the literature for many decades; however, an accepted solution is still lacking.
2 prediction of the Debye model. The physical origin of these universal properties has been lively discussed in the literature for many decades; however, an accepted solution is still lacking.
One of the main reasons for this longstanding debate lies in the experimental difficulties of studying the acoustic excitations in disordered systems in the THz and sub-THz frequency range. As a consequence, the experimental data available in the literature are scarce and often even conflicting. The recent advent of the inelastic X-ray scattering (IXS) technique has opened access to the wave-number (q) and frequency dependence of the longitudinal acoustic excitations in the THz frequency range [2]. However, the IXS experiments are currently limited to q ≥ 1 nm-1 with an instrumental resolution of ~0.3 THz: the (q, ![]() ) region crucial for studying the boson peak remains then close to the edge of the capabilities of the technique. Early IXS results [2] suggested that the longitudinal acoustic excitations in glasses are unaffected across the frequency range where the boson peak appears. More recent results [3] have clarified that they actually experience a regime of strong scattering below the boson peak frequency position where their lifetime very quickly decreases on increasing frequency. Following the continuous development of the IXS technique, we have collected data of unprecedented quality that shed new light on the high frequency dynamics of glasses.
) region crucial for studying the boson peak remains then close to the edge of the capabilities of the technique. Early IXS results [2] suggested that the longitudinal acoustic excitations in glasses are unaffected across the frequency range where the boson peak appears. More recent results [3] have clarified that they actually experience a regime of strong scattering below the boson peak frequency position where their lifetime very quickly decreases on increasing frequency. Following the continuous development of the IXS technique, we have collected data of unprecedented quality that shed new light on the high frequency dynamics of glasses.
 |
|
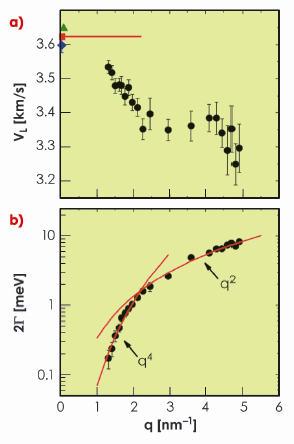
Fig. 20: Wavevector dependence of a) the longitudinal sound velocity and b) the sound attenuation, 2 |
The IXS experiment was carried out on a sample of glassy glycerol at beamline ID16. IXS spectra, characterised by Brillouin peaks corresponding to a longitudinal acoustic excitation, were collected for different q values. As for simple crystals, the frequency position of the maximum of the Brillouin peak divided by q gives a sound velocity. The point here is that this velocity is characterised, at q-values of a few nm-1, by an unexpected and marked decrease (negative dispersion) with respect to the macroscopic value, see Figure 20a. In the same q range, the acoustic attenuation, i.e. the broadening 2![]() of the Brillouin peak, shows a marked increase with a high power of q, and changes slope at a q value, qc, related to the end of the negative dispersion observed in the sound velocity data. This implies that well-defined sound modes for q<qc rapidly lose their plane wave character and transform, on increasing q, into a complex superposition of atomic vibrations. Moreover, qc corresponds to frequencies of ~1 THz, i.e. exactly to the frequency range where the boson peak appears in this glass. This connection between boson peak and high-frequency acoustic excitations can in fact be made quantitative, and clarifies that the boson peak and the aforementioned universal excess over the Debye model prediction found in the specific heat of glasses at temperatures of ~10 K originate indeed from the peculiar acoustic properties of glasses observed here.
of the Brillouin peak, shows a marked increase with a high power of q, and changes slope at a q value, qc, related to the end of the negative dispersion observed in the sound velocity data. This implies that well-defined sound modes for q<qc rapidly lose their plane wave character and transform, on increasing q, into a complex superposition of atomic vibrations. Moreover, qc corresponds to frequencies of ~1 THz, i.e. exactly to the frequency range where the boson peak appears in this glass. This connection between boson peak and high-frequency acoustic excitations can in fact be made quantitative, and clarifies that the boson peak and the aforementioned universal excess over the Debye model prediction found in the specific heat of glasses at temperatures of ~10 K originate indeed from the peculiar acoustic properties of glasses observed here.
In other words, in crystals, the continuum elasticity model holds true on a length-scale much larger than the interatomic spacing and gradually breaks down on approaching the microscopic scale. In glasses, the structural disorder undermines the continuum Debye model in a subtle way: the continuum elasticity theory breaks down abruptly on the mesoscopic length-scale of about ten interatomic spacings characteristic of the medium range order, where it would still work well for the corresponding crystalline systems.
References
[1] W.A. Phillips, Amorphous Solids: Low Temperature Properties (Springer, Berlin, 1981).
[2] F. Sette, M. Krisch, C. Masciovecchio, G. Ruocco and G. Monaco, Science 280, 1550 (1998).
[3] B. Rufflé, G. Guimbrètiere, E. Courtens, R. Vacher and G. Monaco, Phys. Rev. Lett. 96, 045502 (2006).
Principal publication and authors
G. Monaco (a) and V.M. Giordano (a), Proc. Natl. Acad. Sci. USA 106, 3659 (2009).
(a) ESRF



