- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2003
- X-ray Absorption and Magnetic Scattering
- Ab initio Methods to Compute Anapolar Moments in Molecular Systems
Ab initio Methods to Compute Anapolar Moments in Molecular Systems
The anapole moment is defined as the second moment of the current density: ![]() = (
= (![]() /c)
/c) ![]() d3r3j
d3r3j
It was first introduced by Zel'dovich in 1958 to describe parity violating interactions in nuclei. Recent experimental [1]and theoretical [2] studies have shown the importance of such an operator also in the description of non-centrosymmetric crystals.
Non-centrosymmetric systems which have both electric dipole moment (parity mixing) and magnetic dipole moments (unpaired spins) generate an anapole moment. In a relativistic scheme the electronic current is defined as: j = c![]() Ý
Ý ![]()
![]()
where ![]() is the Dirac spin matrix.
is the Dirac spin matrix.
In electronic distributions, the importance of anapolar moments is related to the optical activity of non-centrosymmetric systems. For instance, the X-ray dichroic signals measured on such crystals are characterised by the interference of electric-dipole (E1) and electric-quadrupole (E2) transitions [1]. Recent work by the ESRF Theory Group has led to the development of sum rules [2] that relate the E1-E2 interference signals to the expectation value of the anapole operator that Marri and Carra have defined, in a non-relativistic scheme, in terms of three contributions:
-
pure orbital anapole moment
 L = [nxL Lxn]/2
L = [nxL Lxn]/2 -
pure spin anapole moment
 S = [nxS]
S = [nxS] -
mixed spin-orbital anapole moment
 SL = [[
SL = [[ L,L](2),S](1)
L,L](2),S](1)
The sum rules provide valuable information about edge-selective optical activity; nevertheless they cannot measure the expectation value of the anapole operator.
Owing to the complexity of the mathematical derivations of the second moment of the relativistic current density, analytical estimations of anapolar moments have been performed only on small size systems, ranging from single atoms to model molecules of 4 atoms. Numerical (ab initio) calculations are required in this case.
Within this context, we present the first ab initio calculation of the anapole moment that uses a relativistic formulation of the current density with spin-orbit correction.
The computation uses the Amsterdam Density Functional (ADF) code (www.scm.com). An implemented version, with Dr. E. van Lenthe, University of Amsterdam, allows the computation of the anapole moment in molecular systems. Nevertheless, in order to compare with previous analytical results, we restricted the first applications to a Stark-induced anapole moment on alkali atoms, for which analytical estimations [3]were performed.
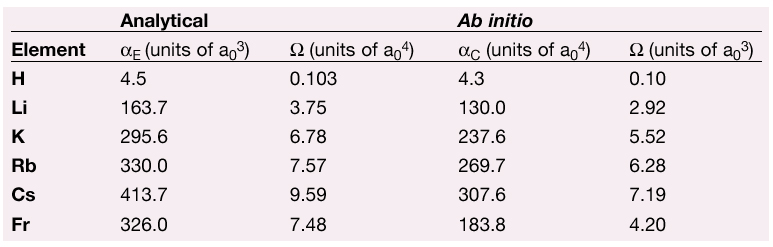
Computed electric polarisabilities ![]() E and anapole moments by the two-component formalism (ADF code) are shown in Table 1 together with the analytical estimations. It should be stressed that estimated results consider neither spin-orbit nor scalar relativistic corrections.
E and anapole moments by the two-component formalism (ADF code) are shown in Table 1 together with the analytical estimations. It should be stressed that estimated results consider neither spin-orbit nor scalar relativistic corrections.
 |
|
Table 1: Estimates for the alkali-metal ground states, polarisability and anapole moment. The first two columns are estimations based on analytical derivations, the last two were computed with the ADF ab initio program. |
 |
|
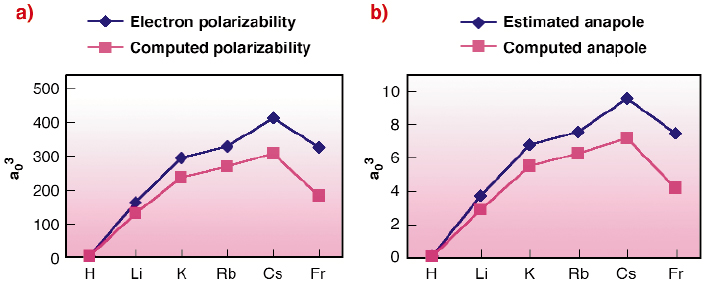
Fig. 116: (a) Electron polarisability for the alkali atoms. Comparison of computed ab initio values and "mixed" estimated and experimental values from ref. [3]; (b) Anapolar moment for the alkali atoms. Comparison of the computed ab initio and estimated values from ref. [3]. |
Estimated and computed values have similar trends (Figure 116). Nevertheless the difference in the absolute value can be attributed to two different factors:
- The computed ab initio anapole includes relativistic corrections that are usually neglected by analytical work. This is coherent with the largest deviation obtained for francium. In this case the relativistic effects are most important and so the approximations used in the analytical development are no longer valid.
- The ab initio electron polarisabilities and anapole moments are very sensitive to the choice of the basis set used for the wavefunction description. Several test are undertaken to optimise the results.
References
[1] J. Goulon, A. Rogalev, F. Wilhelm, C. Goulon-Ginet, P. Carra, D. Cabaret and Ch. Brouder, Phys. Rev. Lett., 88, 237401, (2002) and references therein.
[2] I. Marri and P. Carra, Phys. Rev. B, 69, accepted.
[3] R. Lewis, S.M. Blinder, Phys. Rev. A, 52, 4439 (1995).
Author
V. Vetere
ESRF



