- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2010
- Soft condensed matter
- Jamming kinetics: PNIPA gels
Jamming kinetics: PNIPA gels
Anomalous relaxation behaviour continues to be detected in an increasing number of materials, including glasses, sand piles, and more broadly, jammed systems [1,2]. A striking feature of dense colloidal suspensions and other such disordered crowded systems is their difference from dilute suspensions, where motion is diffusive and fluctuations decay at a rate Γ = Dq2 (q being the momentum transfer and D the diffusion coefficient). In jammed systems, the intensity correlation functions are instead compressed exponentials of the form exp[-Γ(t)n], (n > 1), with hyper-diffusive dispersion relationships Γ~qp, (p ≈ 1). Although microscopic explanations have been advanced for this type of dynamics, the origin of the behaviour is poorly understood.
Jamming was recently identified in the out-of-equilibrium state of poly(N-isopropyl acrylamide) (PNIPA) hydrogels undergoing deswelling. PNIPA hydrogels belong to a class of environmentally sensitive systems that display a volume phase transition (VPT) at a critical temperature TVPT ≈ 34°C, above which they shrink by expelling solvent. Depending on the sample preparation, the rate of shrinkage can be very slow indeed. This stimulus-responsiveness is the basis of numerous medical and industrial applications, for which the contraction time is often of crucial importance. At the VPT, microphase separation occurs promptly, with formation of microscopic polymer surfaces that scatter visible light so strongly that observations of the bulk material by standard dynamic light scattering are excluded. X-ray photon correlation spectroscopy (XPCS), however, offers a unique window for investigating their internal dynamics.
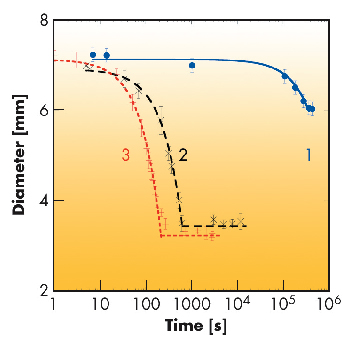
Three different PNIPA gel samples were synthesised with increasing degrees of inhomogeneity. Macroscopic measurements of deswelling were made on the disks by immersing them in water at 50°C and measuring their diameter d with a video camera as a function of time t. The responses exhibit essentially two types of behaviour (Figure 56). Gels containing small amounts of cross-linker deswell extremely slowly, but above a given cross-link content an abrupt increase of some 3 orders of magnitude in their deswelling rate occurs. The disk diameter decreases linearly with time until the equilibrium volume is reached (in the logarithmic scale of the figure, these linear decays appear curved). A linear decay implies that the gel deswells by uniform expulsion of the solvent. All points in the gel thus approach each other with velocity v= αr, where r is the separation between any two points and α, the divergence of the velocity, defines the rate of deswelling. The speckle pattern scattered by the shrinking gel correspondingly moves uniformly outwards to increasingly large values of q. The time required for a speckle to migrate over one pixel of the detector determines the intensity correlation function, g2(t)-1, which decays to zero linearly with time at a rate G that is proportional to q.
 |
|
Fig. 56: Variation of diameter of PNIPA hydrogel disks at 50°C, for samples of increasing cross-link density 1, 2 and 3. Lines are fits to d = d0 - vt, where v is the velocity of the disk at its rim. |
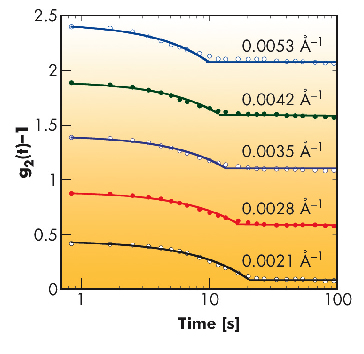
Qualitatively, the linear time dependence predicted for the intensity correlation functions g2(t)-1 (Figure 57) fits well with the XPCS measurements obtained at ID10A on a PNIPA gel (sample 1 in Figure 56) at 50°C. The linear dependence of Γ on q is also recovered.
Quantitatively, the XPCS measurement yields for the deswelling rate at this temperature α = 2.3 10-3 s-1. Owing to the sensitivity of this system to inhomogeneities, the deswelling rate may be accelerated in the X-ray beam, becoming comparable with that of sample 3 in Figure 56, for which the macroscopic deswelling rate is 2.6 10-3 s-1.
 |
|
Fig. 57: XPCS intensity correlation functions of deswelling for a PNIPA gel at 50°C at different q. Lines are fits to the linear decay (1-Γt) with α = 2.3 10-3 s-1. Successive curves vertically offset by 0.5. |
These results show that in PNIPA hydrogels the linear dependence both on t and on q of the intensity correlation function stems from the divergence of the velocity. The same mechanism is also likely to operate in other jammed systems undergoing densification (or expansion), notably colloid suspensions. The associated linear form of the intensity correlation function offers an alternative to the compressed exponential form usually assumed.
Principal publication and authors
K. László (a), A. Fluerasu (b,c), A. Moussaïd (b,d) and E. Geissler (d), Soft Matter 6, 4335-4338 (2010).
(a) Department of Physical Chemistry and Materials Science, Budapest University of Technology and Economics (Hungary)
(b) ESRF
(c) present address: NSLS-II, Brookhaven National Laboratory, Upton, NY (USA).
(d) Laboratoire Interdisciplinaire de Physique, Université J. Fourier de Grenoble (France)
References
[1] A.J. Liu and S.D. Nagel, Soft Matter 6, 2869-2870 (2010).
[2] A.O.N. Siemens and M. van Hecke, Physica A 389, 4255-4264 (2010).



