- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2012
- Soft condensed matter
- Dynamical anisotropy and heterogeneity in a bidimensional gel
Dynamical anisotropy and heterogeneity in a bidimensional gel
What do snow tires share with chocolate and plasters for transdermal drug delivery? The notable properties of all these systems are determined by molecular mobility, which is slowed down by the presence of a dynamical arrest transition. As a matter of fact, molecular mobility determines many of the properties of soft matter systems, particularly in interfacial systems which are retrieved in a wide variety of technologies and products, from paints to food science, and from oil recovery to personal care products. Molecular mobility may be slowed down by a transition to dynamical arrest, often happening without any associated structural transition. To date, there is no unifying theory describing these kinds of dynamical transitions, in marked contrast with “classic” phase transitions, e.g. crystallisation or evaporation, where the underlying mechanisms are well understood. However, there is a broad consensus that transition to dynamical arrest is characterised by heterogeneous, non-Gaussian dynamics [1]. This has become evident in numerical simulation work [2], but direct experimental evidence on real systems is scarce.
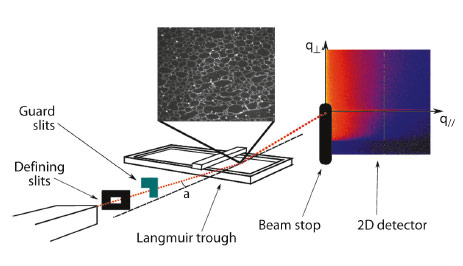 |
|
Fig. 77: Sketch of the setup used for XPCS experiments on Langmuir monolayers. |
Dimensionality is known to play a key role in arrested systems: in a well-known example, hard sphere caging occurs in three dimensions at volume fractions of about 60%–64%, while in two dimensions the random close packing is only attained at a much higher area fraction, about 82%. The system we study here is a two-dimensional gel formed by gold nanoparticles at the air-water interface. The XPCS [3] experiments were performed at beamline ID10A. The high brilliance and stability of the coherent X-ray beam at the ESRF was necessary to obtain data with excellent signal-to-noise ratio from a sample consisting of only one single Langmuir monolayer (see Figure 77). This allowed the intensity autocorrelation function, g(2), to be measured with high accuracy, and the anisotropy of the dynamics to be assessed, which turned out to be completely confined at the air/water interface plane. Moreover, as the interfacial mechanical properties [4] of the same interfacial gel system have been characterised independently, a direct comparison between the rheological properties and the dynamical properties could be made. A model advanced a few years ago by Bouchaud and Pitard [5] proved particularly successful in describing the data. In this model, a relation between the elastic modulus G’ and the characteristic relaxation time of g(2) in elastic soft solids is postulated. Our findings clearly corroborate this hypothesis, as shown in Figure 78a.The good signal-to-noise ratio of the data allowed the four times correlation functions g(4)(q,t1,t2) to be measured for the first time by XPCS, as displayed in Figure 78b, where it is compared with the usual second-order time correlation function g(2)(q,t). Access to g(4) allowed a determination of the lifetime and nature of the dynamical heterogeneity (e.g. avalanches, intermittency, etc.) that characterises the dynamics of this 2-D gel. The right panel of Figure 78c shows the q-dependency of the lifetime of dynamical heterogeneity (open symbols) compared with the relaxation time of the dynamics obtained by g(2). g(4) features a broad peak centred at a characteristic time which is one order of magnitude smaller than the relaxation time of g(2). Both times follow the same qualitative law τ ≈ q-1 which is an experimental finding that challenges the different theoretical frameworks attempting to describe dynamical arrest transitions.
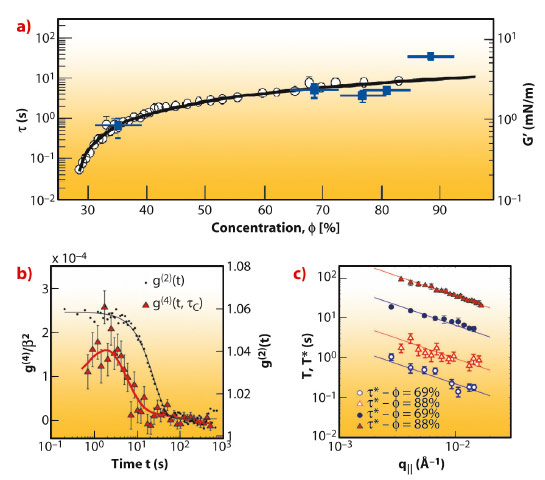 |
|
Fig. 78: a) The relaxation time (blue squares) and the elastic modulus (G’, empty circles) as a function of gel concentration. The theoretical prediction (solid line) is clearly observed in this 2-D gel system. b) first experimental determination of the correlation function g(4). c) The characteristic times for both types of correlation functions share the same dependence on q||, also at different surface concentrations of the gel. |
In summary, the XPCS experiment on a Langmuir monolayer forming a 2-D gel provided detailed insight into the anisotropic dynamics of this system, which is confined at the air-water interface. In particular, the non-Gaussian nature of the dynamical fluctuations was characterised by directly calculating the fourth order temporal correlation function g(4)(q,t1,t2), which thereby was experimentally accessed for the first time by XPCS.
Principal publication and authors
D. Orsi (a), L. Cristofolini (a), G. Baldi (a,b) and A. Madsen (c,d), Phys. Rev. Lett.108, 105701 (2012).
(a) Physics Department, Parma University (Italy)
(b) CNR-IMEM Institute, Parma (Italy)
(c) ESRF
(d) European X-Ray Free Electron Laser, Hamburg (Germany)
References
[1] A. Madsen, R.L. Leheny, H. Guo, M. Sprung and O. Czakkel, New Journal of Physics 12, 055001 (2010).
[2] L. Berthier, Physics 4, 42 (2011).
[3] G. Grübel, A. Madsen and A. Robert, in Soft-Matter Characterization, edited by R. Borsali and R Pecora (Springer, 2008), pp. 935-995.
[4] Interfacial Rheology, edited by R. Miller, L. Liggieri (V S P International Science Publishers) 2009.
[5] J.-P. Bouchaud and E. Pitard, The European Physical Journal E 6, 231-236 (2001).



