- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2012
- Enabling technologies
- PyFAI, a python tool for fast azimuthal integration
PyFAI, a python tool for fast azimuthal integration
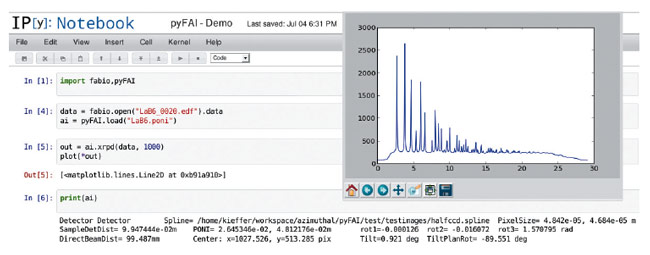
PyFAI [1,2] is a software package designed to reduce SAXS, WAXS and XRPD images recorded by area detectors to 1D plots (azimuthal integration), or 2D patterns (a polar transformation called “caking” or “azimuthal regrouping”). PyFAI is also a software library that can be integrated into other tools like PyMca and EDNA. It also provides a clean python-based interface to enable interactive use from the console, as shown in Figure 144. PyFAI features tools for batch processing and calibration facilities for optimising the geometry of the experiment by using the Debye-Scherrer rings of a reference sample.
 |
|
Fig. 144: Example of interactive use of FabIO and pyFAI in the notebook edition of IPython. |
The geometry used in pyFAI is compatible with any flat area detector at any orientation, even significantly tilted. Moreover geometry configurations can be imported from other tools like FIT2D or SPD. Fast integration is obtained by combining the data processing algorithm, which ensures that each pixel from the detector provides a direct contribution to the final diffraction pattern, with a parallelisation algorithm optimised for modern hardware.
The Python programming language, which is already used in many scientific applications, was chosen for data analysis because it permits rapid testing of new algorithms thanks to the NumPy toolbox and the iPython interface (a free alternative to Matlab). Python allows programs to scale from small scripts to large applications, and can be used with graphical interfaces such as PyMca or MxCube.
Building blocks for X-ray science have been developed at the ESRF such as FabIO [3] for image data access, pyHST for tomographic reconstructions and pyFAI (presented here) for azimuthal regrouping.
Azimuthal integration is a transformation from Cartesian to polar space where the radial dimension can either be the distance (radius), the momentum transfer (q) or the scattering angle (2θ). Throughout this geometrical transformation, total intensities must be conserved in order to obtain quantitatively accurate results (unlike interpolation). Integration is performed via a histogram-like algorithm:
- Each pixel of the image is associated with its polar coordinates, then a pair of histograms versus the radial dimension are built, one unweighted for measuring the number of pixels falling into each bin and another weighted by the pixel intensities.
- Intensities are taken after dark-current subtraction, corrections for flat-field as well as for solid-angle and polarisation effects.
- The diffraction pattern is obtained by dividing the weighted histogram by the number of pixels per bin.
- 2D regrouping is obtained in the same way using two-dimensional histograms over radial and azimuthal dimensions.
- In order to avoid high frequency noise where pixel statistics are low, pixels are split over multiple bins according to their spatial extent.
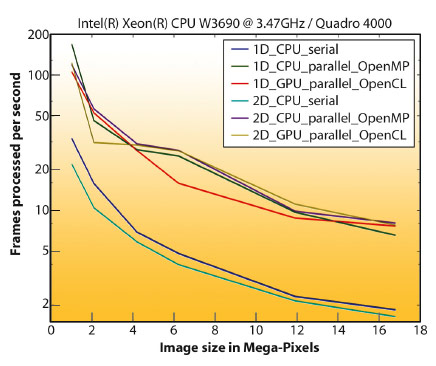
While the histogram build-up technique is efficient on a single processor, it faces write-access conflicts when run in parallel [2] and requires costly locking. This issue was addressed by pre-calculating (and storing) the full correspondence table (or look-up table) between all the image pixels and the histogram bins. Thanks to the look-up table, different output bins can then be processed in parallel making azimuthal integration computationally effective on multi-core systems and on graphics cards. Figure 145 shows the number of frames processed per second versus image size on a typical beamline workstation.
 |
|
Fig. 145: Performances of pyFAI on a beamline (ID13) workstation: frames processed per second versus image size (in mega-pixel). |
Parallel implementations are much faster than their serial equivalents but have a drawback in their larger memory footprint due to the look-up table. The graphic card is used because it is as fast as the processor for this kind of task, and it is a relatively cheaper resource.
The maximum attainable data throughput is in the order of 200 Mpixels/second (800 MBytes/second of float data; much more than the speed of current hard disks), and therefore depends on a computer having a sustained supply of data to be able to continue working at this speed. For a typical image of 2048 x 2048 pixels, and after loading and setting up, pyFAI takes about 20 milliseconds per new frame to compute the 1D integrated profile. However, the sustained rate for integrating large datasets (thousands of images) is only around 100 milliseconds per image due to reading bottlenecks.
PyFAI has been used online on two SAXS beamlines at the ESRF (BM26 – Dubble and BM29 – BioSaxs) since Spring 2012. It is also integrated into Python servers (like EDNA), where it processes images at speeds of up to 1 fps, being mainly limited by the network and disk latencies. To overcome this limitation, pyFAI is currently being integrated into the image acquisition server LImA, providing integrated images directly as output frames from the detector, reaching 30 fps in test conditions. Thanks to the FabIO library [3], pyFAI is compatible with at least 20 detectors formats from 12 different manufacturers. Several ESRF beamlines are interested in this development including ID02, ID11, ID13 and ID22. Other institutes have also shown interest: CEA Grenoble, CEA Saclay and Synchrotron Soleil.
The source code is open source under the GPL license conditions and is available at http://github.com/kif/pyFAI. PyFAI is packaged and available in common Linux distributions like Debian 7.0 and Ubuntu 12.04. Installer packages for Windows and MacOSX can be downloaded from https://forge.epn-campus.eu/projects/azimuthal/files.
Authors
J. Kieffer, D. Karkoulis and J.P. Wright
ESRF
References
[1] J. Kieffer and D. Karkoulis, PyFAI, a versatile library for azimuthal regrouping, Journal of Physics: Conference Series (2013), Accepted (volume: SRI2012).
[2] J. Kieffer and J.P. Wright, PyFAI: a Python library for high performance azimuthal integration on GPU, Powder Diffraction (Proceedings of EPDIC13), Submitted.
[3] E.B. Knudsen, H.O. Sørensen, J.P. Wright, G. Goret and J. Kieffer, FabIO: easy access to 2D X-ray detector images in Python, Journal of Applied Crystallography (2013), Accepted.



