- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2012
- Electronic structure and magnetism
- Iron magnetic moments in-plane on the topological insulator Bi2Se3(111) surface
Iron magnetic moments in-plane on the topological insulator Bi2Se3(111) surface
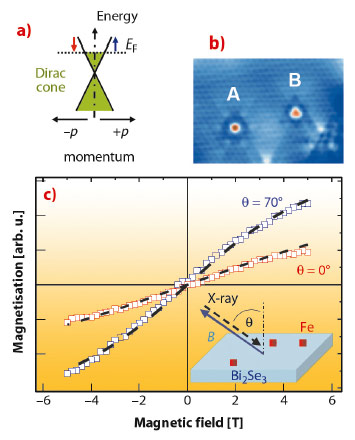
Topological insulators have gained interest from the scientific community as a new class of materials illuminating fascinating yet exotic physics and offering large potential for applications in the field of spintronics [1]. Bulk topological insulators host a 2-dimensional gapless topological surface state with very special properties. An hour-glass shaped dispersion is observed, the so-called Dirac cone, where the energy of the topological surface state increases linearly with the electron momentum p in the (px, py) surface plane (see Figure 95a). In contrast to graphene, where such Dirac cones are also observed, in the topological surface state spin-orbit coupling and time reversal symmetry leads to a locking of both spin and momentum degrees of freedom: two electrons moving in opposite directions (+/– p) must have reversed spins (symbolised as red and blue spins in Figure 95a). One consequence is the suppression of 180° elastic back-scattering electrons in the absence of spin-flip processes, which in principle allows for a high mobility of electrons within the surface plane. An interesting question is the robustness of these “topologically protected” processes against perturbations. It has been suggested that the interaction with magnetic impurities opens a gap at the Dirac point of the topological surface state, provided that the magnetic order is oriented normal to the surface plane and thus breaks the time-reversal symmetry [2]. This mechanism is of critical importance for spin-based transport in such materials.
 |
|
Fig. 95: a) Linear dispersion relation around the Dirac-cone of a topological insulator. b) Low-temperature scanning tunnelling microscopy image of iron atoms on the Bi2Se3 surface. c) XMCD magnetisation curves of iron along two directions θ = 0° and 70° with respect to the surface normal. |
Magnetic properties of iron impurities on a Bi2Se3 surface, a prototypical topological insulator, were studied at ID08 using X-ray magnetic circular dichroism (XMCD) techniques. Figure 95b shows a low-temperature scanning tunnelling microscopy image of isolated iron atoms on the selenium-terminated surface of Bi2Se3. The iron atoms are located on surface fcc and hcp hollow site positions (‘A’ and ‘B’). The iron atoms are deposited on the surface at low temperatures T = 10 K in order to prevent migration of atoms on the surface and cluster formation. A multiplet structure visible in X-ray absorption spectra reflects the high-spin state of single Fe atoms which are influenced by the resultant trigonal crystal fields due to the absorption site.
Figure 95c shows magnetisation curves M versus magnetic field B extracted from XMCD data at the iron L3,2 absorption edges. The magnetisation clearly differs for the two different angles θ = 0° and 70° between the Bi2Se3 surface normal and the X-ray beam direction. Magnetic fields were applied collinear to the X-ray beam as shown in the inset of Figure 95c. The magnetisation curves M(B) show smaller values along θ = 0° demonstrating a preferential orientation in the surface plane. A fit of the experimental magnetisation curves in Figure 95c, using a thermodynamic model which includes the Zeeman term and a magnetic anisotropy term, leads to a significant in-plane magnetic anisotropy energy of 1.9 meV per atom. The observed in-plane anisotropy is supported by DFT calculations if both crystal fields and dynamic hybridisation processes between iron 3d states and the topological insulator are taken into account. As a consequence it is expected that iron tends to leave the topological surface state unperturbed, since the in-plane magnetisation states, which obey time-reversal symmetry, are preferred.
Principal publication and authors
J. Honolka (a), A.A. Khajetoorians (b), V. Sessi (c), T.O. Wehling (b,d), S. Stepanow (a), J.-L. Mi (e), B.B. Iversen (e), T. Schlenk (b), J. Wiebe (b), N.B. Brookes (c), A.I. Lichtenstein (b), Ph. Hofmann (e), K. Kern (a) and R. Wiesendanger (b), Phys. Rev. Lett. 108, 256811 (2012).
(a) Max-Planck-Institute for Solid State Research, Stuttgart (Germany)
(b) University of Hamburg, Hamburg (Germany)
(c) ESRF
(d) Bremen University, Bremen (Germany)
(e) Aarhus University, Aarhus (Denmark)
References
[1] M.Z. Hasan and C.L. Kane, Rev. Mod. Phys. 82, 3045 (2010).
[2] L.A. Wray et al., Nature 7, 32 (2011).



