- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2010
- Soft condensed matter
- Scale-dependent slowdown in a colloidal nematic phase
Scale-dependent slowdown in a colloidal nematic phase
Nematics are the simplest example of a phase with no positional order, but still exhibiting orientational order (and hence anisotropy). This combination endows them with remarkable qualities: although fluid, they have elastic properties and, consequently, long-lived fluctuations. A great deal is known about the large-scale dynamics of nematic systems, which is well described by a generalised hydrodynamic model. However, there is much less data on their short-range behaviour (over length scales comparable to the inter-particle distance) due to a lack of suitable techniques. Understanding the dynamics at this scale, where interaction between particles defines the structure of the system, is essential for building a complete picture of the phase.
X-ray scattering methods are suitable for exploring these distance and time scales. X-ray photon correlation spectroscopy (XPCS) gives access both to the static structure factor S(q) and the collective diffusion coefficient D(q). Based on very general thermodynamic arguments, these parameters are related by D(q) ~ 1/S(q) (“de Gennes narrowing”). In colloidal suspensions, a more refined treatment must take into account the hydrodynamic interactions, which further modulate this dependence through a hydrodynamic function H(q) = S(q)xD(q)/D0 (where D0 is the diffusion coefficient at infinite dilution).
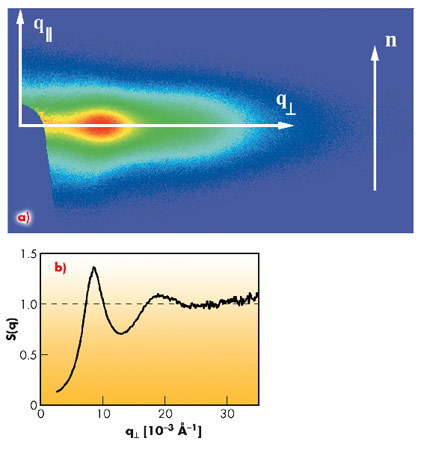
We measured the hydrodynamic function for a fluid nematic phase of goethite (α-FeOOH) nanorods (with an aspect ratio of about ten). The experiments were performed at ID10A using an X-ray energy of 8 keV, in the uniform filling mode of the storage ring. The scattered signal was detected by a two-dimensional Maxipix detector consisting of 256x256 pixels, and the intensity autocorrelation functions were calculated by ensemble averaging over equivalent pixels. A typical SAXS pattern of an aligned nematic sample is displayed in Figure 58a. We show in Figure 58b the corresponding structure factor S(q⊥), along the direction perpendicular to the director n (which indicates the average orientation of the particles).
 |
|
Fig. 58: a) SAXS pattern of an aligned nematic sample. The arrow indicates the direction of the nematic director n. b) Structure factor along the q⊥ direction calculated from the SAXS data in (a). |
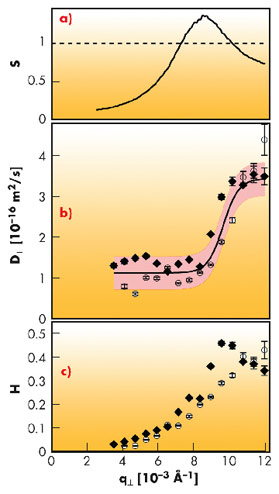
We recorded the time correlation function g(t) of the scattered signal and analysed it to obtain the relaxation rate Ω. The diffusion coefficient is obtained as D(q) = Ω (q)/q2. The static and dynamic data, as well as the hydrodynamic function H(q) defined above, are presented in Figure 59. Unexpectedly, we found that, below the position of the structure maximum, D decreases sharply by more than a factor of three with respect to its high-q (i.e. short distance) value (Figure 59b); the fit with a sigmoidal function is also shown. Combined with the decrease of S(q) in the same range (Figure 59a), this yields a hydrodynamic slowing down (decrease of H(q) in Figure 59c) by a factor of ten, much stronger than that seen in hard sphere suspensions, a result that emphasises the strength of hydrodynamic interactions in reduced dimensions.
In summary, we measured for the first time the dynamics of a colloidal nematic phase down to the inter-particle distance, revealing non-trivial and scale-dependent hydrodynamic effects, namely a reduced collective diffusion coefficient at long distances. The onset of the slowing down corresponds rather well to the position of the peak in the structure factor. Therefore, our experiments suggest a crossover between two different kinds of behaviour at scales smaller and larger than the inter-particle distance, raising the fundamental (and very difficult) question of the transition between the microscopic level of the individual particles to the macroscopic one described by continuum theories.
Principal publication and authors
A.S. Poulos (a), D. Constantin (a), P. Davidson (a), B. Pansu (a), É. Freyssingeas (b), A. Madsen (c) and C. Chanéac (d), Journal of Chemical Physics 132, 091101 (2010).
(a) Laboratoire de Physique des Solides, Orsay (France)
(b) Laboratoire de Physique ENS-Lyon, Lyon (France)
(c) ESRF
(d) Laboratoire de Chimie de la Matière Condensée, Paris (France)