- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2009
- Dynamics and extreme conditions
- Lattice dynamics of stishovite from powder inelastic X-ray scattering
Lattice dynamics of stishovite from powder inelastic X-ray scattering
Elastic and thermodynamic properties of minerals play a central role in Earth science, and are required to obtain insight into pressure-temperature stability fields and the validity of geochemical models. Quantities such as specific heat, entropy, free energy, Debye temperature and velocity can in principle be derived from the vibrational density of states (VDOS). The complete momentum resolved lattice dynamics, however, provides much more information, e.g. all components of the elastic stiffness tensor. An often encountered major obstacle to overcome in order to obtain the complete set of phonon dispersion curves is that conventional inelastic X-ray (IXS) and neutron scattering (INS) approaches require single crystals. In a previous work we have shown that this limitation can be overcome by recording IXS spectra from polycrystalline materials over a sufficiently large momentum transfer (Q) range, and to interpret them using an adjustable force constant model [1]. Here, we apply this methodology to the case of stishovite, a high pressure SiO2 polymorph. Stishovite has been chosen as a benchmark case, since (i) its geophysical relevance is currently discussed in relation to the seismic signature of the X-discontinuity at a depth about 300 km [2], and (ii) there is no complete experimental data set for its lattice dynamics.
The IXS spectra were recorded at beamline ID28 between Q = 3.9 nm–1 and 54.8 nm–1 with an overall energy resolution of 3 meV. As nine IXS spectra at different Q-values are recorded simultaneously, the desired Q-range could be covered with only three spectrometer settings, with a total data acquisition time of two days. Lattice dynamics calculations were performed using CASTEP software employing density functional perturbation theory in its DFT-GGA version.
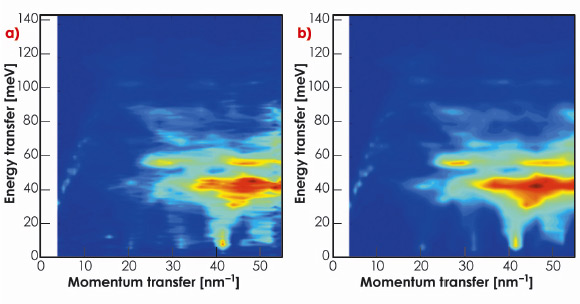
The excellent agreement between the experimental and theoretical data can be appreciated in Figure 23, which displays the energy (E) and momentum transfer (Q) dependence of the inelastically-scattered intensity. We emphasise that a single scaling factor was applied to the theoretical energy scale. Furthermore, the validity of the model is proven for any crystallographic direction, as orientation averaging probes the low-symmetry directions as well. Relative intensities of phonons are naturally embedded in the experimental spectra thus providing the instrument to check the consistency of the phonon eigenvectors within the model. The phonon dispersion for high symmetry directions naturally appears as a by-product (see principal publication).
 |
|
Fig. 23: (E-Q) intensity maps for polycrystalline stishovite: a) experiment; b) calculation. Elastic line subtraction and renormalisation are applied to the experimental spectra; the energy axis of the calculated map is scaled by a factor 1.05. |
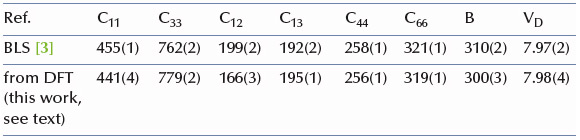
The agreement of elastic moduli derived from the DFT-GGA calculation by the stress-strain method with those determined experimentally from Brillouin light scattering was significantly improved by rescaling the sound velocity, density and cell shape, where scaling factors were derived from comparison of calculations to the experimental polycrystalline data. A significant deviation (~20%) remains for C12, while all other moduli and the integral properties (bulk modulus B and Debye velocity VD) converge very well (see Table 1), thus confirming the predictive power of DFT-GGA stress-strain calculations.
 |
|
Table 1: Comparison of elastic moduli Cijj and bulk modulus B (in GPa) and Debye velocity VD (in km/s) with the most recent data set from Brillouin light scattering (BLS). |
To obtain the elastic anisotropy from polycrystalline data makes the employed approach attractive for Earth science. When the anisotropy of individual phases is known, the macroscopic anisotropy observed in many parts of the Earth can be related to the preferable orientation pattern. While the current study is limited to ambient pressure and temperature, an extension to high pressures is feasible. This would allow the derivation of reliable elastic and thermodynamic data for materials such as polycrystals that cannot be quenched to ambient conditions and can only be synthesised in minute amounts, e.g. in a diamond anvil cell.
References
[1] I. Fischer, A. Bosak and M. Krisch, Phys. Rev. B. 79, 134302 (2009).
[2] Q. Williams and J. Revenaugh, Geology 33, 1-4 (2005).
[3] F. Jiang, G.D. Gwanmesia, T.I. Dyuzheva and T.S. Duffy, Physics of the Earth and Planetary Interiors 172, 235-240 (2009).
Principal publication and authors
A. Bosak (a), I. Fischer (a), M. Krisch (a), V. Brazhkin (b), T. Dyuzheva (b), B. Winkler (c), D. Wilson (c), D. Weidner (d), K. Refson (e) and V. Milman (f), Geophysical Research Letters 36, L19309 (2009).
(a) ESRF
(b) Institute for High Pressure Physics RAS, Troitsk Moscow region (Russia)
(c) Geowissenschaften, Goethe-Universität, Frankfurt a.M. (Germany)
(d) Mineral Physics Institute, Stony Brook University, Stony Brook (USA)
(e) Rutherford-Appleton Laboratory, Chilton, Didcot (UK)
(f) Accelrys, Cambridge (UK)



