- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2009
- Dynamics and extreme conditions
- Sound velocity in iron carbide (Fe3C) at high pressure
Sound velocity in iron carbide (Fe3C) at high pressure
The Earth’s core is thought to be made of iron alloyed with light elements [1]. The inclusion of light elements is required to account for the discrepancies in density and sound wave velocity between seismological models and pure Fe or Fe–Ni alloys. Carbon is one of the possible alloying elements; its stability in carbides is greatly enhanced at high pressure. Extrapolation to inner core pressures indicates that iron carbide Fe3C would crystallise preferentially to the classical high-pressure phase of iron (hcp), which could make Fe3C a major phase in the Earth’s inner core [2].
A linear dependence of longitudinal acoustic (LA) velocity as a function of density holds for many iron alloy compounds. This provides a way to compare sound velocity properties of pure iron or iron alloyed compounds with seismological models for the Earth’s core [3]. Our idea was to estimate the relative abundance of Fe3C in the Earth’s core, not only on the basis of density comparison but also by using acoustic sound velocity measurements. Such measurements can be obtained at high pressure using the inelastic X-ray scattering (IXS) technique. We have thus collected IXS spectra to 83 GPa on a synthetic polycrystalline sample of Fe3C in a diamond-anvil cell. Sound velocities were measured at high pressure by very high resolution IXS at ID28, with an incident photon energy of 15.817 keV and a total instrumental energy resolution of 5.5 meV full width at half maximum.
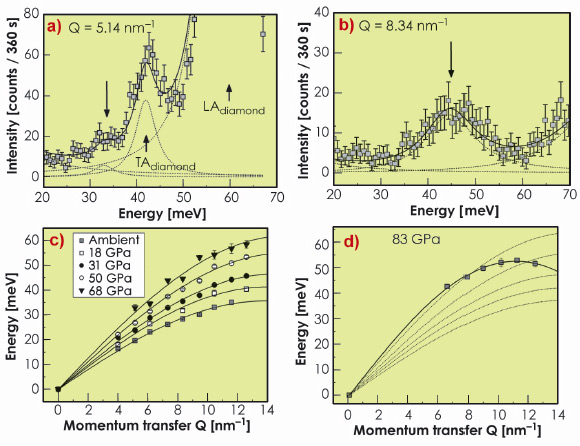
IXS patterns (Figures 21a and 21b) are characterised by an elastic contribution, centred at zero energy, and an inelastic contribution from an LA mode from Fe3C and a transverse acoustic (TA) phonon from diamond visible at low Q values. The dispersion curves presented in Figures 21c and 21d can be well described by a sine function. Such a sine fit made to the experimental dispersion then yields the average LA velocities for the high-pressure aggregate.
 |
|
Fig. 21: a) and b) IXS spectra of a polycrystalline Fe3C sample at 68 GPa for selected momentum transfers Q. The experimental data are shown along with the best fit results to the dataset (solid line) and the corresponding individual components (thin dotted line and arrow). c) Dispersion curves for polycrystalline Fe3C to 68 GPa. d) Experimental points and dispersion curve (solid line) obtained at a pressure of 83 GPa showing a clear softening of the longitudinal acoustic branch at high Q. |
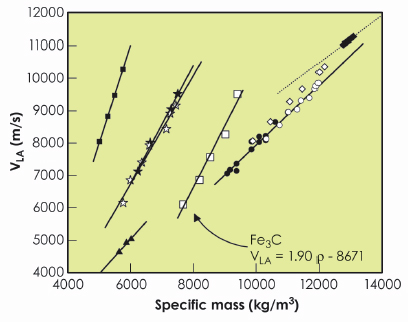
At pressures exceeding 70 GPa, we also observed anomalous behaviour in the dispersion curve. The IXS data collected at 83 GPa (Figure 21d, bottom) indeed displays a strong softening of the LA branch, which could correspond to a second-order magnetic transition as proposed from theoretical calculations [4]. At lower pressures, the observed increase of the phonon frequencies corresponds to an increase of the longitudinal wave velocity (VL) from 6100 to 9375 ms–1. Angle-dispersive X-ray diffraction patterns were also collected in order to obtain the molar volume and hence, the density. Sound velocities and corresponding densities of Fe3C are reported in Figure 22, along with results obtained for other iron light element alloys [3]. The longitudinal wave velocity of Fe3C scales linearly with its density. We then used a simple model to describe the average density and the longitudinal velocity VL of a two-component ideal solid, combined with a known thermal equation of state for pure iron, to estimate the optimal amount of light element Fe3C in the alloy.
 |
|
Fig. 22: LA velocities of Pnma Fe3C as a function of density (hollow squares), along with results obtained for other light elements alloyed with pure iron. Solid squares: FeS2 pyrite; hollow stars: FeSi; solid stars: FeO; solid triangles: phase IV FeS, circles: pure iron. Data are compared with seismic observations for the liquid outer core (hollow diamonds) and solid inner core (solid diamonds). See [3] for further details. |
Assuming that our sound velocity model holds for low light element contents, and that the magnetic transition may be shifted to higher pressures for low carbon content, the main result is that about 1 wt% carbon in the solid inner core could account for the difference between the measured longitudinal velocity and density, and the seismological Earth’s inner core data. With silicon also shown to be abundant in the solid core [3], we are thus left with silicon and carbon as possible alloyed light elements to be further investigated in the Fe-Si-C ternary system.
References
[1] F. Birch, J. Geophys. Res. 57, 227–286 (1952).
[2] B. Wood, Earth Planet. Sci. Lett. 117, 593–607 (1993).
[3] J. Badro, G. Fiquet, F. Guyot, E. Gregoryanz, F. Occelli, D. Antonangeli and M. d’Astuto, Earth Planet. Sci. Lett. 254, 233–238 (2006).
[4] L. Voãadlo, J. Brodholt, D.P. Dobson, K.S. Knight, W.G. Marshall, G.D. Price and I.G. Wood, Earth Planet. Sci. Lett. 203, 567–575 (2002).
Principal publication and authors
G. Fiquet (a), J. Badro (a), E. Gregoryanz (b), Y. Fei (c) and F. Occelli (d), Phys. Earth Planet. Int. 172, 125-129 (2009).
(a) Institut de Minéralogie et de Physique des Milieux Condensés (IMPMC), Université Pierre et Marie Curie, CNRS, Université Paris Diderot, Institut de Physique du Globe de Paris (France)
(b) Centre for Science at Extreme Conditions (CSEC), University of Edinburgh (UK)
(c) Geophysical Laboratory, Carnegie Institution of Washington, Washington DC (USA)
(d) Département de Physique Théorique et Appliquée, CEA, Bruyères-le-Châtel (France)



