- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2008
- Methods and instrumentation
- Capturing the shape of macromolecular crystals in 3D
Capturing the shape of macromolecular crystals in 3D
Absorption correction algorithms have been used for decades, in particular by crystallographers. The first approaches to reduce the effects of absorption were made by physically reshaping the sample to reach simple geometries, such as spherical or cylindrical, so that tabulated corrections could be applied easily. When the crystal could not be reshaped, Albrecht’s [1] method was widely used, it relies on a precise description of the crystal geometry in order to determine the correction graphically.
However, macromolecular crystallography (MX) demanded a different approach. During MX experiments an undefined volume of cryoprotectant buffer is used to hold the macromolecular crystal within a nylon or Kapton loop prior to vitrification and data collection at cryotemperatures (100 K). Such a complex system, often with highly irregularly shaped crystals, is almost impossible to characterise manually with a description of all of the elements contributing to the absorption process, particularly the liquor surrounding the crystal. Most scaling software used in MX today employs an entirely empirical function which minimises the differences between symmetry-equivalent reflections to correct for absorption effects (as well as for the correlated crystal decay and beam effects). With the use of increasingly fragile samples having high radiation sensitivity, complete and redundant data sets may not be obtainable from a single crystal, in turn defeating the fully empirical method. Other methods are therefore needed to optimise such data sets – of particular importance where small signals are being recorded, such as anomalous data from sulphur or phosphorus atoms that commonly occur naturally in proteins or nucleic acids.
Studies on two methods to supply three-dimensional shape information recorded directly from the cryocooled crystals in vitrified buffer and supporting loop have been carried out. One uses the standard visible-light microscope systems installed on all of the ESRF MX beamlines to build a three-dimensional model based on reconstruction from shape-from-silhouettes of the crystal, buffer and loop components; the second uses X-ray microtomography to determine the three-dimensional shape of the crystal within its surrounding liquid and sample holder.
Visible light silhouettes
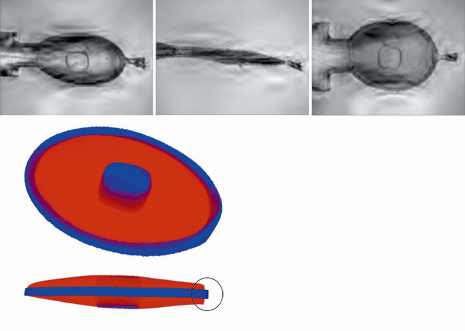
The key aim behind this method is to provide a routine system to build three-dimensional models of the crystal-buffer-loop system by exploiting a standard on-axis sample visualisation system that incorporates a high-quality on-axis camera system for sample alignment. As part of this development, a software suite (called “3DAC”) was developed specifically to reconstruct the 3D model and calculate absorption correction factors using the 2D images from the camera. A feasibility study was carried out on an insulin crystal from which diffraction data were collected at low energy (6 keV). A high quality three-dimensional model was constructed using just 18 visible-light images at different rotation angles of the sample (Figure 160) with the loop, buffer and crystal silhouettes determined using a mixture of automatic and manual procedures. Absorption corrections were determined based on simulated beam paths through the 3D model that consisted of the three separate loop, buffer and crystal components. The corrections were applied to each reflection (whether partially or fully recorded) before merging.
A comparison of the reduced data resulting from the standard empirical approach to scaling MX data and application of the absorption corrections calculated as above showed a distinct and significant improvement in the data when our corrections were applied. Metrics such as the Rmerge, signal:noise ratio and peak heights in phased anomalous difference maps all improved when data having a redundancy of less than approximately three was used. For example, in the best cases, average peak heights corresponding to sulphur positions in the phased anomalous map improved by 10% to 60% depending upon the redundancy of the data (from higher to lower redundancy). The exact effect observed depended on the wedge of diffraction data used, i.e. the orientation of the crystal-loop system. However, the best data were consistently obtained with application of the quantitative absorption correction.
 |
|
Fig. 160: (top) Examples of the composite images built from visible light images taken at different focal lengths to overcome depth-of-field issues; (lower) The three-dimensional model of the insulin crystal, buffer and loop built from the images. Blue shows the crystal and loop components, and red the cryocooled buffer. The circle on the lower image shows where minor errors are apparent in the model. |
X-ray microtomography
In X-ray tomography, a 3D reconstruction of the sample is obtained after collecting parallel-beam X-ray images at a series of rotation angles. At higher energies (> 5 keV), macromolecular samples typically show very little absorption contrast between the vitrified crystal and its surrounding liquid. Fortunately, one can exploit phase contrast which results in a sample to detector distance-dependent enhancement of the edges between crystal, liquor and sample support.
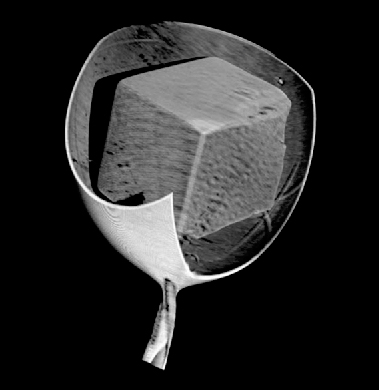
We have successfully applied the technique of X-ray microtomography to obtain 3D reconstructions of a variety of protein and DNA crystals (Figure 161). The great advantage of the technique is that a true “X-ray” view of the crystal is obtained, showing details such as cracks, crystal splitting and satellites, bent crystals and other imperfections. The reconstruction algorithms benefit from existing methods such as those used in electron tomography.
X-ray microtomography leads to superior views of the macromolecular sample and its support compared to visible-light methods, however, it does require a special imaging setup. The X-ray beam has to fully bathe the sample, and a carefully aligned X-ray imaging detector is needed. We have demonstrated that such a setup, which is default on imaging beamlines, can also be successfully installed and used on a macromolecular crystallography beamline. The doses needed to obtain X-ray tomographic data could stay within a few percent of the Henderson limit, especially if one does not require sub-micrometre resolution. This would make the technique amenable for absorption correction as well as for crystal alignment.
 |
|
Fig. 161: Full three-dimensional reconstruction of a vitrified lysozyme crystal and surrounding cryocooled buffer from X-ray tomography. |
In conclusion, both studies have shown the feasibility of producing and using three-dimensional models of macromolecular crystals and their supporting buffer and loop to improve diffraction data quality. Each method has its own pros and cons, but give complementary information. The tomography method gives stunning models, accurate down to the tiniest details but requires a specific, purpose-built installation. The visible-light method uses standard beamline equipment but produces a model showing only the overall bulk of the crystal, buffer and loop. The methods should provide a clear advantage in situations where data acquisition is limited by crystal lifetime and should form an essential component of sample characterisation on future beamlines, as part of the overall complete characterisation of the macromolecular crystal. Three-dimensional shape information can also have a practical impact on the design of data collection strategies for X-ray diffraction experiments and for neutron studies. Further work is now concentrating on expanding the number of test cases and comparing the absorption corrections obtained from the two modelling approaches. Given the increasing interest in radiation damage and the study of ever more sensitive macromolecular systems, the time is now right to revive the implementation of fully non-empirical absorption corrections through easy-to-use (even automatic) methodologies.
Principal publications and authors
R.M.F. Leal (a,b,c), S.C.M. Teixeira (b,c), V. Rey (a), V.T. Forsyth (b,c) and E.P. Mitchell (a,c); J. Appl. Cryst. 41, 729-737 (2008); S. Brockhauser (d), M. Di Michiel (a), J.E. McGeehan (d), A.A. McCarthy (d) and R.B.G. Ravelli (d,e); J. Appl. Cryst. 41, 1057-1066 (2008).
(a) ESRF
(b) ILL (France)
(c) EPSAM and ISTM, Keele University (UK)
(d) EMBL, Grenoble Outstation (France)
(e) Leiden University Medical Center (LUMC) (The Netherlands)
Reference
[1] G. Albrecht, Rev. Sci. Instrum., 10, 221–222 (1939).



