- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2007
- Soft Condensed Matter
- Slow dynamics and ageing in colloidal gels studied by XPCS
Slow dynamics and ageing in colloidal gels studied by XPCS
Aggregation and gelation are topics of fundamental interest in condensed matter physics [1] that also have many direct industrial applications. Delayed sedimentation is a non-equilibrium phenomenon encountered in a variety of soft-matter systems, including colloidal suspensions with sufficiently strong short-ranged attractive interactions. Due to the interactions, the colloidal particles can aggregate at relatively low concentrations (e.g. 20%) to form a space-filling structure often denoted as a gel. However, this non-equilibrium structure slowly evolves, until the spatial connectivity is lost and the gel suddenly collapses.
In this work we have used X-ray photon correlation spectroscopy (XPCS) to study the slow dynamics in a colloidal transient gel consisting of a mixture of polymethylmethacrylate (PMMA) nano-particles with a radius R = 1070 Å and non-adsorbing random-coil polystyrene (PS) dispersed in cis-decalin. The addition of polymers causes an effective attraction between the colloids via the so-called depletion mechanism [1] and leads to the formation of the gel. The XPCS experiments were performed using partially-coherent X-rays at beamline ID10A (Troïka). The scattering (speckle images) from the PMMA/PS gels were recorded by a direct illumination CCD with 22 µm pixels located 2.3 m downstream of the sample. Series of several thousand CCD frames were taken and the dynamic properties were investigated by calculation of two-time correlation functions,
![]()
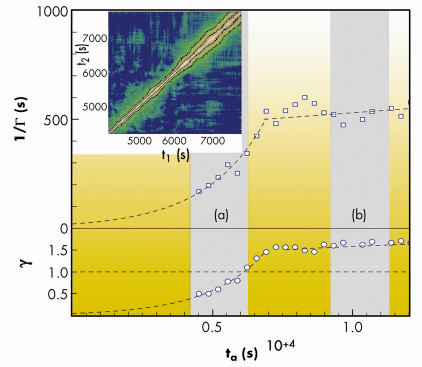
Where ‹› denotes an ensemble average performed over many pixels of the CCD detector. The natural variables to describe the two-time correlation functions (see inset in Figure 53) are the average time or “age” ta=(t1+t2)/2, measured by the distance along the t1=t2 diagonal and the time difference t=|t1-t2| which is the distance from the t1=t2 diagonal in the perpendicular direction. The widening of the two-time correlation contour plots (Figure 53, inset) is indicative of an ageing process. The correlation times become increasingly longer with time (age). To quantify this phenomenon, the two time correlation functions were averaged over narrow, equal-age, slices. This leads to more common (albeit age dependant) “one-time” correlation functions. Unlike the case of simple Brownian motion where the correlation functions are well described by simple exponential decays, here a Kohlrausch (or “stretched exponential”) form has to be used,
g(Q,t) ![]() exp[–2(
exp[–2(![]() t)
t)![]() ]
]
The fitting parameters, the relaxation rate ![]() and the exponent
and the exponent ![]() are both age (ta) and Q-dependent. The age-dependence of
are both age (ta) and Q-dependent. The age-dependence of ![]() and
and ![]() , calculated for a single wave vector Q corresponding to a value of QR=3 are shown in Figure 53. After an initial stage (ta< 7000s) during which the correlation times increase exponentially with age, a region with huge fluctuations is entered. We attribute these strong fluctuations to large scale rearrangements in the gel. Such behaviour has been observed previously in different systems and a universal model for ageing in soft matter was proposed [2]. A remarkable crossover from
, calculated for a single wave vector Q corresponding to a value of QR=3 are shown in Figure 53. After an initial stage (ta< 7000s) during which the correlation times increase exponentially with age, a region with huge fluctuations is entered. We attribute these strong fluctuations to large scale rearrangements in the gel. Such behaviour has been observed previously in different systems and a universal model for ageing in soft matter was proposed [2]. A remarkable crossover from ![]() <1 to
<1 to ![]() >1 can be observed during the early stages of the process. While relaxations with
>1 can be observed during the early stages of the process. While relaxations with ![]()
![]() 1 have been found before in several different systems, it is, to our knowledge, the first time that such an evolution with age is observed. Since compressed exponential relaxations (
1 have been found before in several different systems, it is, to our knowledge, the first time that such an evolution with age is observed. Since compressed exponential relaxations (![]() >1) have been found in putative jammed states, our measurements may indicate a jamming transition occurring during the initial stages of the delayed sedimentation process.
>1) have been found in putative jammed states, our measurements may indicate a jamming transition occurring during the initial stages of the delayed sedimentation process.
 |
|
Fig. 53: Correlation times 1/ |
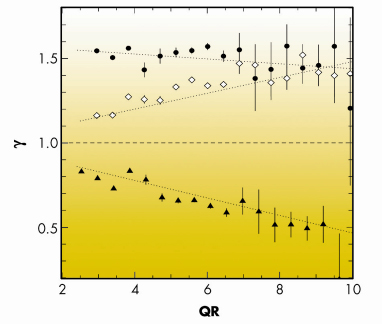
The age- and Q-dependent g exponents can better be seen in Figure 54. While at the early stages they are sub-unitary on all length scales (filled triangles), the picture changes in the full-ageing regime, where the relaxations are better described by compressed exponentials (![]() ~ 1.5). This indicates that the system is jammed on all the probed length scales. Interestingly, towards the final stages of the gel lifetime (diamonds), the situation changes again and the low-Q
~ 1.5). This indicates that the system is jammed on all the probed length scales. Interestingly, towards the final stages of the gel lifetime (diamonds), the situation changes again and the low-Q ![]() exponents start approaching unity. This is indicative of an “un-jamming” process on large length scales preceding the final gel collapse.
exponents start approaching unity. This is indicative of an “un-jamming” process on large length scales preceding the final gel collapse.
 |
|
Fig. 54: |
References
[1] K.N. Pham, A.M. Puertas, J. Bergenholtz, S.U. Egelhaaf, A. Moussaïd, P.N. Pusey, A.B. Schofield, M.E. Cates, M. Fuchs, W.C.K. Poon, Science, 296, 104 (2002).
[2] L. Cipelletti, L. Ramos, S. Manley, E. Pitard, D.A. Weitz, E.E. Pashkovski and M. Johansson, Faraday Disc., 123, 237 (2003).
Principal publication and authors
A. Fluerasu (a), A. Moussaïd (a), A. Madsen (a), A. Schofield (b), Phys. Rev. E 76, 010401(R) (2007).
(a) ESRF
(b) Dept. of Physics & Astronomy, University of Edinburgh (UK)



