- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2007
- Materials Science
- High-resolution powder diffraction and electron microscopy - a powerful combination
High-resolution powder diffraction and electron microscopy - a powerful combination
Determination of a crystal structure from powder diffraction data is no longer a rarity thanks to impressive methodological advances in recent years. However, some problems have remained intractable. A case in point is that of the zeolite catalyst IM-5, whose structure eluded determination for almost ten years.
Over the years, high-resolution powder diffraction data had been collected on several different samples of IM-5 on BM01B, the SNBL beamline at the ESRF and on the materials science beamline at SLS. None of the samples were ideal: all contained impurities, none had particularly sharp peaks, and diffraction intensity decreased markedly with diffraction angle. Nonetheless, by comparing the different IM-5 patterns, the peaks corresponding to the IM-5 phase could be distinguished from those of the various impurities, and a tentative indexing of the patterns was achieved (C-centred orthorhombic with a = 14.299 Å, b = 57.413 Å and c = 20.143 Å). This was subsequently confirmed via electron diffraction.
This open-framework silicate has an unusually large unit cell, with a volume almost triple that of ZSM-5, which is one of the most complex zeolites known. There are also approximate relationships between the axes (b ~ 4a and c ~ ![]() 2a), so symmetrically unrelated reflections have very similar d-spacings. These factors result in an enormous degree of reflection overlap, which is the key hindrance to structure solution from powder diffraction data. Of the 4120 reflections in the pattern, 3499 are within 0.2 FWHM of a neighbouring reflection with which it therefore overlaps. The pattern with the sharpest peaks, an identified impurity (analcime) and the largest range of d-spacings (SNBL,
2a), so symmetrically unrelated reflections have very similar d-spacings. These factors result in an enormous degree of reflection overlap, which is the key hindrance to structure solution from powder diffraction data. Of the 4120 reflections in the pattern, 3499 are within 0.2 FWHM of a neighbouring reflection with which it therefore overlaps. The pattern with the sharpest peaks, an identified impurity (analcime) and the largest range of d-spacings (SNBL, ![]() =0.99995Å, collected in 1998) was selected for further analysis.
=0.99995Å, collected in 1998) was selected for further analysis.
The key to structure solution for another complex zeolite, (TNU-9), had proven to be the inclusion of crystallographic phases derived from high-resolution electron microscopy (HRTEM) images [1], so it was reasoned that a similar approach might also work for IM-5. In the case of TNU-9, the zeolite-specific program Focus had been used, but for IM-5 we decided to test the (material independent) powder charge-flipping (pCF) approach [2]. Both algorithms work in both real and reciprocal space, so information can be added easily in either realm. Phases for 95 reflections were derived from HRTEM images taken along three different directions and input to the program Superflip. Although there were some promising looking channel systems in some of the resulting electron density maps, detailed interpretation was not possible.
Meanwhile, a model had been derived from the HRTEM images, but its geometry was strained and its powder diffraction pattern did not match the experimental data very well, even after refinement. Speculating that this model was probably at least partially correct, it was used to calculate starting phase sets for pCF (instead of random phases). The phase of each reflection calculated from the structure was varied by up to 25% in a random fashion, thereby generating 1000 different starting points for 1000 distinct pCF runs. The best five electron density maps were then merged, and interpretation of the resulting map was almost trivial (Figure 45). Refinement of this structure converged with the R-values RF = 0.075 and Rwp = 0.188 (Rexp = 0.142).
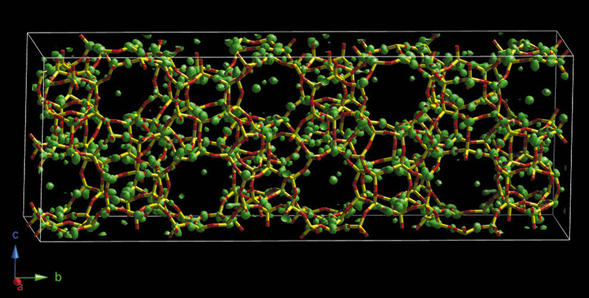 |
|
Fig. 45: Electron density map from pCF that was used to derive the structure of IM-5. |
As suggested by catalytic tests, the IM-5 framework structure has a 2-dimensional 10-ring channel system with effective pore widths ranging from 4.8 to 5.5 Å. This channel system is unusual in that it also has a limited third dimension (Figure 46), giving it the character of a 3-dimensional one with complex channel intersections that can accommodate bulky intermediates in catalytic reactions, while retaining the overall effect of a 2-dimensional one with long-range diffusion restricted to just two dimensions.
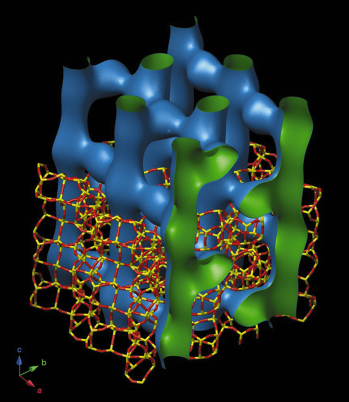 |
|
Fig. 46: The unusual 2-dimensional 10-ring channel system of IM-5. |
There are 24 topologically distinct Si atoms in the asymmetric unit. This translates to 864 atoms (288 Si + 576 O) in the unit cell. Because no symmetry is assumed in charge flipping, the number of atoms per unit cell rather than the number per asymmetric unit is the prime limitation of the algorithm. This implies that the structures of other polycrystalline materials with similar numbers of atoms per unit cell, whatever their chemical composition, should also be accessible via this route, providing that high-resolution powder diffraction data and suitable HRTEM images can be obtained.
References
[1] F. Gramm, Ch. Baerlocher, L.B. McCusker, S.J. Warrender, P.A. Wright, B. Han, S.B. Hong, Z. Liu, T. Ohsuna, O. Terasaki, Nature, 444, 79-81 (2006).
[2] Ch. Baerlocher, L.B. McCusker, L. Palatinus, Z. Kristallogr. 222, 47-53 (2007).
Principal publication and authors
Ch. Baerlocher (a), F. Gramm (a), L. Massüger (a), L.B. McCusker (a), Z. He (b), S. Hovmöller (b), X. Zou (b), Science, 315, 1113-1116 (2007).
(a) Laboratory of Crystallography, ETH Zurich (Switzerland)
(b) Structural Chemistry, Stockholm University (Sweden)



