- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2007
- High Resolution and Resonance Scattering
- Dielectric function of silicon for finite momentum transfer
Dielectric function of silicon for finite momentum transfer
Modern theoretical solid state physics often aims to understand the properties of materials by means of numerical calculations which do not use parameters taken from experiment. The starting point of these ab initio calculations for many-electron systems is mostly the well-established static density-functional theory (DFT). For many spectroscopic quantities (which are always connected to the response of the system to a time-dependent perturbation), the time-dependent density-functional theory (TDDFT) [1] can be employed. One of its important ingredients is the so-called exchange-correlation kernel fxc that represents the electron-electron interactions in the response beyond a simple Hartree picture (where only the classical Coulomb potential is varied). It is a complicated quantity, the exact expression of which is unknown, and which has to be approximated. To this end, close interaction of theory and experiment is essential.
The design of good approximations is closely linked to the identification of the relevant physical effects. One of the most widely used approximations, in particular for finite systems like molecules, is the adiabatic local-density approximation (ALDA, also called TDLDA), although it fails for the optical absorption spectra of bulk materials, i.e., in the long-wavelength limit in extended systems. We, by contrast, investigate the situation of finite momentum transfers.
We performed inelastic X-ray scattering (IXS) measurements on beamline ID16. Using monochromatic X-rays of 7.909 keV and a Si wafer with the normal parallel to the [110] direction, the dynamic structure factor, proportional to the loss function, was measured for momentum transfers between 0.27 and 2.40 a.u. along the [111] and [100] directions. The energy resolution was 1.1 eV; no additional features were observed in the spectra upon increase in resolution to 0.2 eV.
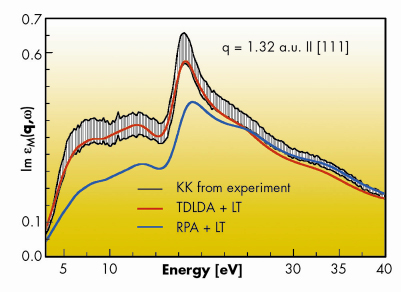
We find that the TDLDA improves greatly upon the result in the random-phase approximation (RPA, where fxc is neglected altogether and only the induced Hartree potential is considered). Comparison between theory and experiment led to the conclusion that the TDLDA describes the valence excitations very well provided that lifetime effects are added. The latter is done under the assumption that the lifetimes of the electrons and holes created in the system, calculated on a one-quasi-particle level, are essentially independent. The excellent agreement between experiment and theory shows that lifetime effects are not contained in the TDLDA but can be added separately.
Moreover, we have extracted the dielectric function from the measured structure factor by means of the Kramers-Kronig relations, which connect the real and the imaginary part of the dielectric function. In Figure 9 we show its imaginary part. The good result of the TDLDA stands in contrast to its performance in the optical limit (vanishing momentum transfer) where the dielectric function calculated in TDLDA is far from experiment.
 |
|
Fig. 9: Imaginary part of the dielectric function extracted from the measured dynamic structure factor using the Kramers-Kronig (KK) relations and compared to the TDLDA and the RPA calculations, both with added lifetime (LT) effects. The shaded area shows the error bar of the extraction. |
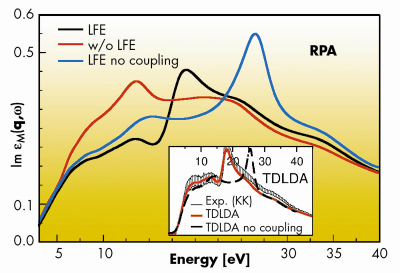
The excellent agreement between experiment and theory allowed for the identification of important effects. We could elucidate the role of an important mixing between single interband transitions, that is, transitions between states calculated within the simple independent-particle picture. This mixing is due to induced Hartree and exchange-correlation potentials, with components of the wavelength of the perturbation and other components. These other components give rise to the so-called local-field effects (LFE) which are mediated by the microscopic inhomogeneity of the material and shown in Figure 10. Unlike in the optical spectra of bulk silicon, their influence is strong. Moreover, we compare with a calculation that neglects the coupling of the transitions of positive energy with transitions of negative energy. Our results show that this coupling is very important, although often neglected (Tamm-Dancoff approximation), and this in contrast to optical spectra.
 |
|
Fig. 10: Influence of local- field effects (LFE) for the RPA spectra of Figure 9, and influence of the coupling with the transitions of negative energy. The inset shows the influence of the coupling for the TDLDA. |
In conclusion, thanks to the close interaction of theory and experiment we have been able to determine the approximation adequate for the description of valence excitations in semiconductors for finite momentum transfer. The combination of TDLDA and electron and hole lifetime effects yields spectra of predictive quality. Moreover, we could elucidate the role of the microscopic inhomogeneity of the material for the coupling of otherwise independent transitions. The connection of state-of-the-art experiment with theoretical investigations has thus greatly improved our understanding of electronic excitations in semiconductors.
References
[1] S. Botti, A. Schindlmayr, R. Del Sole, and L. Reining, Rep. Prog. Phys. 70, 357-407 (2007).
Principal publication and authors
H.-Ch. Weissker (a,d), J. Serrano (b), F. Bruneval (a,d), F. Sottile (a,d), S. Huotari (b), G. Monaco (b), M. Krisch (b), V. Olevano (c,d), and L. Reining (a,d), Phys. Rev. Lett. 97, 237602 (2006).
(a) LSI UMR 7642, CNRS-CEA/DSM, Ecole Polytechnique, Palaiseau (France)
(b) ESRF
(c) Institut NEEL, CNRS, Grenoble (France)
(d) European Theoretical Spectroscopy Facility (ETSF)



