- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2007
- High Resolution and Resonance Scattering
- Structural and collisional relaxations in liquids and supercritical fluids
Structural and collisional relaxations in liquids and supercritical fluids
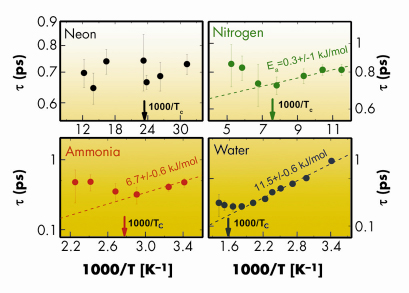
Relaxation processes in fluids have fascinated scientists for many years and remain, to date, a matter of debate. Despite intense efforts, the microscopic origin of these processes still eludes a comprehensive understanding. Among the various relaxations, the structural relaxation is the one related to cooperative rearrangements of the local structure. It is characterised by a relaxation time, ![]() , with a strong (typically Arrhenius) temperature dependence resembling that of viscosity. Recent studies performed on hydrogen bonded (HB) systems suggest that the microscopic mechanism responsible for the structural relaxation is the making and breaking of the hydrogen bonded network, which occurs on the picosecond timescale [1]. The aim of the work presented here was to investigate how this relaxation is affected by the transition from the liquid to the supercritical state. In order to evidence any possible common phenomenology, four systems (neon, nitrogen, ammonia and water), characterised by different intermolecular interactions and intramolecular structures, were studied. The relaxation time was experimentally determined by analysing inelastic X-ray scattering spectra taken at beamlines ID16 and ID28 (further details on the data analysis are reported in [2]). The values obtained for
, with a strong (typically Arrhenius) temperature dependence resembling that of viscosity. Recent studies performed on hydrogen bonded (HB) systems suggest that the microscopic mechanism responsible for the structural relaxation is the making and breaking of the hydrogen bonded network, which occurs on the picosecond timescale [1]. The aim of the work presented here was to investigate how this relaxation is affected by the transition from the liquid to the supercritical state. In order to evidence any possible common phenomenology, four systems (neon, nitrogen, ammonia and water), characterised by different intermolecular interactions and intramolecular structures, were studied. The relaxation time was experimentally determined by analysing inelastic X-ray scattering spectra taken at beamlines ID16 and ID28 (further details on the data analysis are reported in [2]). The values obtained for ![]() are reported in Figure 1. Data belonging to the liquid phase (i.e. for T<Tc, with Tc being the critical temperature) can be empirically described by an Arrhenius law:
are reported in Figure 1. Data belonging to the liquid phase (i.e. for T<Tc, with Tc being the critical temperature) can be empirically described by an Arrhenius law: ![]() =
=![]() 0exp(Ea/kBT). This allowed the activation energy (Ea) of the relaxation to be derived, which was found similar to the energy of the respective intermolecular bonds. In the case of neon the data above Tc are too sparse and dispersed to draw any conclusions.
0exp(Ea/kBT). This allowed the activation energy (Ea) of the relaxation to be derived, which was found similar to the energy of the respective intermolecular bonds. In the case of neon the data above Tc are too sparse and dispersed to draw any conclusions.
From Figure 1, one can also appreciate that, above Tc, the Arrhenius behaviour is lost. This suggests that, on approaching the supercritical state, the role of intermolecular bonds as the leading microscopic mechanism responsible for the relaxation is progressively reduced. In order to quantitatively compare data from different systems, the mean free time between intermolecular collisions, <![]() >, was utilised as a scaling parameter.
>, was utilised as a scaling parameter.
 |
|
Fig. 1: Structural relaxation time, |
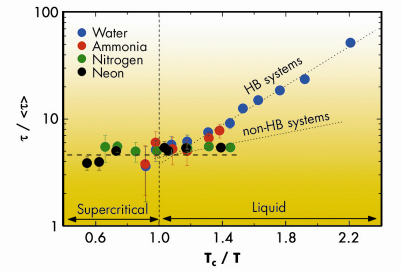
Figure 2 reports the dimensionless quantity ![]() /<
/<![]() > as a function of Tc/T. It can be readily observed that, close and above Tc,
> as a function of Tc/T. It can be readily observed that, close and above Tc, ![]() /<
/<![]() > is constant and similar for all systems. This suggests that the dynamics of the system above Tc is dominated by collisions. On the other hand, below Tc, data for hydrogen bonded and non-hydrogen bonded systems split into two different curves. This can be explained considering that (i) on lowering the temperature a larger number of bonds can be established, and (ii) a stronger attractive potential (as the one of hydrogen bonded systems) increases their lifetime. This difference disappears above Tc, where the role of attractive interactions is strongly reduced.
> is constant and similar for all systems. This suggests that the dynamics of the system above Tc is dominated by collisions. On the other hand, below Tc, data for hydrogen bonded and non-hydrogen bonded systems split into two different curves. This can be explained considering that (i) on lowering the temperature a larger number of bonds can be established, and (ii) a stronger attractive potential (as the one of hydrogen bonded systems) increases their lifetime. This difference disappears above Tc, where the role of attractive interactions is strongly reduced.
 |
|
Fig. 2: Values of |
In conclusion, the comparative study of these four prototype fluids across the liquid-to-supercritical transition reveals major changes in the microscopic mechanism responsible for the observed relaxation process. More specifically, in the liquid phase the leading mechanism is the making and breaking of intermolecular bonds. However, as soon as supercritical conditions are reached, binary collisions rule the microscopic dynamics of the system, as witnessed by the scaling of the data according to the mean free time between intermolecular collisions. These results provide an intuitive picture of the liquid-to-supercritical transition from a microscopic point of view since it was found that, with increasing the temperature, the lifetime of intermolecular bonds decreases to become, close to Tc, shorter than the average time between intermolecular collisions. As a consequence, the time needed for a molecule to get close to another one and eventually to form a new intermolecular bond becomes shorter than the average lifetime of the bond itself, thus preventing the fluid system from developing an extended bond network, typical of the liquid phase.
References
[1] See, e.g., G. Monaco, A. Cunsolo, G. Ruocco and F. Sette, Physical Review E, 60, 5505 (1999).
[2] F. Bencivenga, A. Cunsolo, M. Krisch, G. Monaco, G. Ruocco and F. Sette, Physical Review E, 75, 051202, (2007).
Principal publication and authors
F. Bencivenga (a,b), A. Cunsolo (c), M. Krisch (a), G. Monaco (a), L. Orsingher (d), G. Ruocco (e), F. Sette (a), and A. Vispa (f), Physical Review Letters, 98, 085501 (2007).
(a) ESRF
(b) Now at Sincrotrone Trieste S.C.p.A., Trieste (Italy)
(c) OGG c/o ILL, INFM-CNR, Grenoble (France)
(d) Università di Trento (Italy)
(e) Università di Roma ‘La Sapienza’ (Italy)
(f) Università di Perugia (Italy)



