- Home
- Users & Science
- Scientific Documentation
- ESRF Highlights
- ESRF Highlights 2006
- Materials Science
- Atom location in quasicrystals from atomic pair distribution function refinement
Atom location in quasicrystals from atomic pair distribution function refinement
Quasicrystals have been found in many intermetallic alloy systems in the last 20 years. Their unique feature is the non-crystallographic diffraction symmetry such as 10/mmm or m-3-5. Due to the presence of discrete Bragg peaks they are classified as aperiodic crystals which can be described in higher dimensional (nD, n > 3) space. Their structure and electronic, magnetic, thermal, dynamic, mechanical and surface properties as well as their applications such as thin films have been of great interest in the last years [1]. Special interest has been paid to the Mg-Zn-rare-earth systems where the presence of 4f-elements like holmium raises a question for quasiperiodic magnetic order. Icosahedral Ho11Mg15Zn74 (Figure 24) represents a promising candidate as it provides a primitive 6D space group Pm-3-5 or P235 allowing for such order. Its atomic structure determination is an essential prerequisite for any magnetic structure analysis.
Since quasicrystals are not periodic in 3D space, their structure determination is not trivial. Complementary to the higher dimensional crystallography, we use the real space pair distribution function (PDF) from total scattering powder data (local crystallography). This technique, well established for the structure analysis of glasses, has also been applied to the local structure determination of a number of crystalline but disordered systems [2].
 |
|
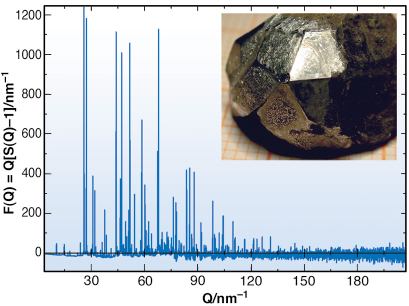
Fig. 24: P-type icosahedral Ho11Mg15Zn74: 41 keV total scattering data F(Q) collected at ID31. The inset shows a cm-sized single crystal of triacontahedral morphology, point group m-3-5. |
The PDF G(r) is a direct Fourier transform of the scattering factor F(Q) = Q[S(Q)-1] where S(Q) is the corrected and normalised X-ray powder scattering intensity, dependent on the scattering vector length Q. G(r) = 4![]() r [
r [![]() (r)-
(r)-![]() 0] gives the probability of finding pairs of atoms separated by the distance r referenced with respect to the average electron density
0] gives the probability of finding pairs of atoms separated by the distance r referenced with respect to the average electron density ![]() 0. It is weighted by the respective Z of the involved atoms. The F(Q) of Ho11Mg15Zn74 from high-resolution data collected at ID31 is shown in Figure 24. The selected energy of 41 keV offers a Qmax = 300 nm-1 which ensures a high resolution of the experimental PDF in real space. In turn, high resolution for Q at ID31 provides a minimal exponential decay of the PDF, consequently there are still sharp peaks at r > 10 nm reflecting long-range quasiperiodic order. The corresponding PDF up to r < 2 nm is displayed in Figure 25.
0. It is weighted by the respective Z of the involved atoms. The F(Q) of Ho11Mg15Zn74 from high-resolution data collected at ID31 is shown in Figure 24. The selected energy of 41 keV offers a Qmax = 300 nm-1 which ensures a high resolution of the experimental PDF in real space. In turn, high resolution for Q at ID31 provides a minimal exponential decay of the PDF, consequently there are still sharp peaks at r > 10 nm reflecting long-range quasiperiodic order. The corresponding PDF up to r < 2 nm is displayed in Figure 25.
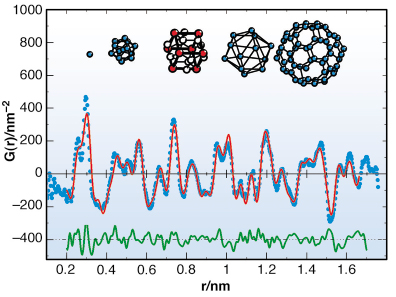
Structure solution is based on trial and error matching of PDFs of known related periodic alloy phases to the experimental data. In this case the PDF of cubic Al23Mg40Zn37 resembles well that of the quasicrystal. Our model for P-type Ho11Mg15Zn74 fits the experimental PDF nicely up to 2.5 nm after least-squares refinements have been performed using G(r) in the interval 0.2 nm < r < 1.8 nm. Figure 25 contains the measured and calculated PDFs and their difference.
 |
|
Fig. 25: Refined local structural model: Experimental (blue dots), model (red line) and difference (green line) PDF data. Inset: onion-like concentric shell model of the basic building block. Mg, Zn, Ho-atoms are marked in white, blue and red, respectively. |
We find that the single atoms in the Ho11Mg15Zn74 quasicrystal are coordinated normally like in the Frank-Kasper phases, which are a well understood class. On a higher hierarchical level, the basic building block is a “stuffed bucky ball” of diameter d ~ 1.5 nm, this is sketched in Figure 25. It is composed like an onion by a concentric arrangement of icosahedra, a pentagon-dodecahedron with an inscribed cube and one central atom. In between neighbouring balls, which share atoms of the outer shell, so-called “glue atoms” can be located. The centres of the balls make up a 3D network defining the next hierarchy level (d ~ 5 nm) in the structure.
To conclude, detailed local atomic models for icosahedral Mg-Zn-rare-earth quasicrystals have been refined from ID31 high resolution powder diffraction data via PDF and yield real atoms, credibly coordinated at credible interatomic distances. Since the PDF simultaneously is a local (< 0.4 nm), medium (nm) and long-range (> 10 nm) probe, regardless of the samples degree of crystallinity, it serves as a versatile experimental function in real space to model atomic structures. Thus in this case the PDF tells us “where the atoms are” in any patch, of selectable size, in the quasicrystal structure.
References
[1] H.R. Trebin (ed.); Quasicrystals, Wiley-VCH (2003).
[2] T. Egami and S.J.L. Billinge; Underneath the Bragg Peaks, Pergamon (2003).
Principal Publication and Authors
S. Brühne (a,b), E. Uhrig (a), K.-D. Luther (a), W. Assmus (a), M. Brunelli (c), A.S. Masadeh (d) and S.J.L. Billinge (d), Z. Kristallogr. 220, 962-967 (2005).
(a) FB Physik, JWGU Frankfurt am Main (Germany)
(b) FB Chemie, JWGU Frankfurt am Main (Germany)
(c) ESRF
(d) Physics Department, MSU, East Lansing (USA)



